Skorobogatov: Counterexamples to the Hasse Principle...

This is joint work with Laura Basile.

We work over a field $k$ with ${\mathrm{char}}k=0$, $\overline{k}$ its algebraic closure.

Definition. A bielliptic surface $X$ is a $\overline{k}/k$-form of a smooth projective surface of Kodaira dimension 0 that is not $K3$, neither abelian nor Enriques.

There is a complete list of such available. We have $K_X \neq 0$, but $nK_X=0$, for $n=2,3,4$ or $6$. Over the algebraic closure, $\overline{X}=E \times F/\Gamma$, where $\Gamma$ acts on $E'$ by translations.

Proposition. There exists an abelian surface $A/k$, a principal homogeneous space $Y$ of $A$, and a finite étale morphism $f: Y \to X$, $\deg f=n$.

Proof. Since $nK_X=(g)$, then consider $t^n=g$ and normalize; the map is unramified, so $K_Y=f^*K_X=0$. By the classification of surfaces, $\overline{Y}$ is an abelian surface. ($f$ is a torsor under $\mu_n$.) $\qedsymbol$

Remark. This will not hold in higher dimension; there are just many more possibilities.

Consider $A=E \times F$, $Y=C \times D$, $C$ a principal homogeneous space of $E$, and likewise $D$ for $F$. Now $\mu_n$ acts on $Y$ so that $\mu_n$ acts on $D$ by translations, $\mu_n \subset F$; the action on $\mu_n$ on $C$ cannot be by translations or else $X$ itself would be a principal homogeneous space, so the action has fixed points.

Proposition. $[C] \in {\mathrm{img}}(H^1(k,E^{\mu_n}) \to H^1(k,E))$.

Proof. Take $\overline{x} \in C(\overline{k})$, fixed by $\mu_n$, and write down the usual cocycle: if $g \in {\mathrm{Gal}}(\overline{k}/k)$, $g\overline{x}-\overline{x} \in E^{\mu_n}(\overline{k})$.

(It arises from $[C^{\mu_n}]$.) $\qedsymbol$

Corollary. Let $\alpha:E \to E_1$ be the isogeny with kernel $E^{\mu_n}$. Then $[C] \in H^1(k,E)[\alpha_*]$.

We have one of the following possibilities:

$$\begin{array}{c\vert c} n & \char93 E^{\mu_n} \\ \hline 6 & \text{$1$\ (so $C(k) \neq \emptyset$)} \\ 4 & 2 \\ 3 & 3 \\ 2 & 4 \end{array}$$

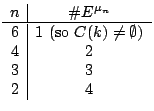
Now assume $k=\mathbb{Q}$, and $X(\mathbf A_\mathbb{Q})=\prod_v X(\mathbb{Q}_v)$; we want an example where $X(\mathbf A_\mathbb{Q})^{{\mathrm{Br}}} \neq \emptyset$, but $X(\mathbb{Q})=\emptyset$. We do the case $n=3$.

With the notation as above:

Theorem. Assume that:

1. ${\mathrm{Gal}}(\overline{\mathbb{Q}}/\mathbb{Q})$ acts nontrivially on $E^{\mu_3}$, which is $\cong \mathbb{Z}/3\mathbb{Z}$ as an abstract group;
2. $\char93$$(E)[\alpha_*]=3$;
3. $[C] \in$   $(E)[\alpha_*]$;
4. $\mu_3 \subset F$;
5. ${\mathrm{Sel}}(F,\mu_3)=0$, that is, for any principal homogeneous space of $F$ obtained from a class in $H^1(\mathbb{Q},\mu_3)$, there exists a place $v$ where it has no point.

Then $X=(C \times F)/\mu_3$ is a counterexample to the Hasse principal not explained by the Manin obstruction.

Example. If $C:x^3+11y^3+43z^3=0$, $\mu_3$ acts by $(x:y:z) \mapsto (x:y:\zeta_3 z)$, $F=D:u^3+v^3+w^3=0$, with $\mu_3$ acting by $(u,v,w) \mapsto (u:\zeta_3 v:\zeta_3^2 w)$; looking at the Selmer group, you look at principal homogeneous spaces of the form $u^3+av^3+a^2u^3=0$, so if $p \mid a$, this has no $\mathbb{Q}_p$ point.

We have ${\mathrm{Br}}\overline{X}={\mathrm{Hom}}(NS(\overline{X})_{{\mathrm{tors}}},\mathbb{Q}/\mathbb{Z})$ as Galois modules (this holds more generally if $X$ is a surface and $h^{2,0}=0$), and $NS(\overline{X})_{{\mathrm{tors}}}=E^{\mu_3}$. Then (i) implies that $({\mathrm{Br}}\overline{X})^{{\mathrm{Gal}}(\overline{\mathbb{Q}}/\mathbb{Q})}=0$.

The kernel of the restricted Cassels pairing $(E)[\alpha_*] \times$   $(E)[\alpha_*] \to \mathbb{Q}/\mathbb{Z}$ consists of elements in the image of $(E_1) \xrightarrow{\alpha_*^t}$   $(E)$, where $\alpha^t:E_1 \to E$ is the dual isogeny. Since $(E)[\alpha_*] \cong \mathbb{Z}/3\mathbb{Z}$ must be zero because it is alternating, so lift $C_1 \to C$; then we have étale maps

$$C_1 \times F = Y_1 \to C \times F=Y \to X;$$

to find an adelic point, find a rational point $R \in F(\mathbb{Q})$ and a collection $\{P_v\} \in C_1(\mathbf A_\mathbb{Q})$; then $f_1:Y_1 \to X$ has $f_1^*({\mathrm{Br}}_1 X) \subset \pi^*({\mathrm{Br}}F)$, where $\pi:Y_1 \to F$ is the projection.

The last condition (v) says that there are no rational points on $X$; rational points on $X$ comes from twists of $Y$, but by assumption these have no point over a place $v$, so they arise from .

Back to the main index for Rational and integral points on higher dimensional varieties.