Salberger: Arithmetic Bezout and Rational Points of Bounded Height

We take the height function

$$H:\mathbb{P}^n(k) \to \mathbb{R}_{>0}$$

$$x=(x_0:\dots:x_n) \mapsto \prod_v \sup_{0 \leq i \leq n}\vert x_i\vert _v$$

If $X \subset \mathbb{P}^n$ is a closed subvariety over $k$, $U \subset X$ an open subvariety also over $k$, we have the counting function

$$N(U,B)=\char93 \{x \in U(k):H(x) \leq B\}.$$

Already the case of smooth cubic surfaces, away from the $27$ lines, this conjecture would imply linear growth, but it was only known recently for quadratic growth; therefore this is hard enough, looking for asymptotic formulas is often asking for too much.

Recently, there has been work which also works in low dimension (curves and surfaces), due to Heath-Brown (2002); this also has applications to other problems (e.g. Waring's problem).

Theorem. [Heath-Brown] Let $X_d \subset \mathbb{P}^n$ be an absolutely irreducible curve of degree $d$; then

$$N(X_d,B) \ll_{n,d,\epsilon} B^{2/d+\epsilon}.$$

The implicit constant does not depend on $X_d$; the results of Faltings have no uniformity. We have applications to surfaces. This result is also best possible, taking the Veronese embedding of $\mathbb{P}^1$. There was a result of Bombieri-Pila which proved $\ll_{d,\epsilon} B^{1+1/d+\epsilon}$. Broberg treats arbitrary number fields $k$ (and the case $n>3$).

This theorem relies on the following result, which is Theorem 14 in the paper of Heath-Brown.

Theorem. [Theorem 14] Let $X_d \subset \mathbb{P}^n$ be an absolutely irreducible projective $\mathbb{Q}$-variety of dimension $r$ defined by forms of degree $\leq \delta$. Let $\epsilon>0$, $B \geq 1$ be given. Then there exists a $\mathbb{Q}$-hypersurface $Y \subset \mathbb{P}^n$ such that:

1. $X_d \not\subset Y$;
2. All $\mathbb{Q}$-points on $X_d$ of height $\leq B$ lie on $Y$;
3. We have
   $$\deg(Y) \ll_{n,\delta,\epsilon} B^{\frac{r+1}{d^{1/r}}+\epsilon};$$

4. The irreducible components of $Y$ have degrees bounded in terms of $n,\delta,\epsilon$.

Remark. Heath-Brown treats only the case $r=n-1$. Taking $r=1$, the result of Heath-Brown is an immediate consequence of this theorem if one applies Bezout's theorem in the plane. The case $r<n-1$ is due to Broberg, and with arbitrary $k$.

If $X$ is smooth, then you may replace $\delta$ by $d$ in (iii) and (iv).

Lemma. [Colliot-Thélène] Let $X_d \subset \mathbb{P}^3$ be a smooth projective surface. Then there exists at most $\ll_d 1$ curves of degree $d-2$ on $X$.

This implies that a cubic has only finitely many lines, a quartic has only finitely many conics, and so on. This is best possible, for $d-1$ one might have infinitely many such curves, for example, infinitely many conics on a cubic surface. Removing these curves, we still have a surface, and we get:

Theorem. [Heath-Brown] Let $X_d \subset \mathbb{P}^3$ be a smooth projective surface and let $U$ be the complement of all curves of degree $\leq d-2$. Then

$$N(U,B) \ll_{d,\epsilon} B^{\frac{3}{\sqrt{d}}+\frac{2}{d-1}+\epsilon}.$$

This is the best known result if $d \geq 6$. To do this, apply Theorem 14 by cutting with an auxiliary hyperplane; the same implicit constant applies everywhere, the $B^{3/\sqrt{d}+\epsilon}$ is the maximum number of irreducible components. We considering for example the Veronese embedding of the projective plane to see that we would expect $\ll B^{3/\sqrt{d}+\epsilon}$.

Theorem. [S] Let $X_d \subset \mathbb{P}^n$ be a smooth absolutely irreducible projective $\mathbb{Q}$-variety of dimension $r$ defined by forms of degree $\leq \delta$. Let $\epsilon>0$, $B \geq 1$ be given. Then there exists a $\mathbb{Q}$-hypersurface $Y \subset \mathbb{P}^n$ such that:

1. $X_d \not\subset Y$;
2. All $\mathbb{Q}$-points on $X_d$ of height $\leq B$ lie on $Y$;
3. We have
   $$\deg(Y) \ll_{n,\delta,\epsilon} B^{\frac{r+1}{rd^{1/r}}+\epsilon}.$$

For the moment, it is not clear how to use this theorem to deduce $\ll B^{3/\sqrt{d}+\epsilon}$.

Proof. Let $Q_1(x),\dots,Q_m(x)$ be monomials in $x=(x_0,\dots,x_n)$ which form a basis of

$${\mathrm{img}}(H^0(\mathbb{P}^n,\mathscr{O}(D)) \to H^0(X,\mathscr{O}(D))),$$

where $D \sim B^{(r+1)/(rd^{1/r})+\epsilon}$. Let $P_1,\dots,P_\ell \in \mathbb{A}^{n+1}(\mathbb{Z})$ represent the $\mathbb{Q}$-points on $X_d$ of height $\leq B$. We need to show that the rank of the matrix

$$\begin{pmatrix} Q_1(P_1) & \dots & Q_1(P_\ell) \\ \vdots & \ddots & \vdots \\ Q_m(P_1) & \dots & Q_m(P_\ell) \end{pmatrix}$$

is $<m$. This is trivial if $m>\ell$; otherwise, we must look at all sub $(m \times m)$-determinants. Since these points are of bounded height, each term in the determinant is bounded by $B^D$, so one has a bound on the archimedean height of the determinant. With more points, the determinants are divisible by high powers of prime numbers (by the Weil conjectures, points must coincide); under certain circumstances, these divisibilities contradict the bounds on the determinant. We use for example that

$$\sum_{p \leq R}\frac{\log p}{p} \sim \log R.$$

This gives the result. $\qedsymbol$

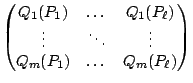
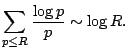
Remark. The theorem is also true for surfaces with at most rational double points. Already, the theorem is not known for elliptic singularities.

We apply this theorem to count $\mathbb{Q}$-points on $X_d \cap Y$ when $\dim X_d=2$. Then $\deg(Y) \ll_{d,\epsilon} B^{3/(2\sqrt{d}) + \epsilon}$. By the adjunction formula (and Bezout),

$$\char93 (X_d \cap Y)_{\text{sing}}(\mathbb{Q}) \ll_d \deg(Y)^2 \ll B^{3/\sqrt{d}+\epsilon}.$$

All $\mathbb{Q}$-points on irreducible, not absolutely irreducible components are singular. Therefore it suffices to count smooth $\mathbb{Q}$-points on absolutely irreducible components of $X_d \cap Y$. Let $Z_1,\dots,Z_s$ be absolutely irreducible components of $X_d \cap Y$ of degree $\leq f(d,\epsilon)$, then

$$\sum_{i=1}^{s}\char93 N(Z_i,B) \ll_{d,\epsilon} (\textstyle{\sum}_i \deg Z_i)B^{(2/e)+\epsilon}$$

where $e=\min \deg(Z_i)$. This is

$$(\textstyle{\sum}_i \deg Z_i)B^{(2/e)+\epsilon} \ll_{d,\epsilon} B^{3/(2\sqrt{d})+2/e+\epsilon}.$$

If you throw out curves of smallest degree, this is smaller than $\ll B^{3/\sqrt{d}}$.

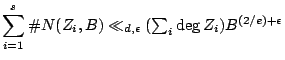
But we still must deal with curves of high degree, e.g. the case when $X_d \cap Y$ is irreducible.

Lemma. Let $Z_\delta \subset \mathbb{P}^n$ be an absolutely irreducible degree $\delta$, and $p$ a prime $\gg_{n,\epsilon} B^{(2/\delta)+\epsilon}$. Then:

1. The number of $\mathbb{Q}$-points on $Z_\delta$ of height $\leq B$ which specializes to a given smooth $\mathbb{F}_p$-point on $Z_\delta$ is $\ll_{n,\epsilon} \delta$.
2. The number of $\mathbb{Q}$-points on $Z_\delta$ with smooth specialization at $p$ is $\ll_{n,\epsilon} \delta B^{(2n/\delta)+\epsilon}$.

Corollary. We have

$$\char93 N(Z_{\delta,\text{smooth}},B) \ll_{n,\epsilon} \delta^4 B^{(2n/\delta)+\epsilon}.$$

If we could replace $\delta^4$ by $\delta^2$, then we would have get $N(U,B) \ll B^{(3/\sqrt{d})+\epsilon}$. It might still be useful to find something like $\delta^{5/2}$. Using arithmetic Bezout, bounding the heights of the subvarieties (due to Faltings), this might succeed. It would also be better to work systematically with all primes $p$, some savings might arise.

Back to the main index for Rational and integral points on higher dimensional varieties.