Cox Rings
This follows an exposition due to Hu and Keel (Yi Hu and Seán Keel, Mori dream spaces and GIT, Michigan Math. J., 48 (2000), 331-348). Let
![]() , and
, and ![]() a projective smooth variety over
a projective smooth variety over ![]() . Let
. Let
![]() be line bundles on
be line bundles on ![]() . If
. If
![]() , then
, then
![]() .
.
We have a multiplication map
![]() . We have a ring
. We have a ring
![]() , which is often not finitely generated.
, which is often not finitely generated.
If
![]() are (semi)ample (a semiample bundle is a pullback of an ample bundle), then
are (semi)ample (a semiample bundle is a pullback of an ample bundle), then
![]() is finitely generated.
is finitely generated.
Definition.
Let ![]() be smooth and projective, and assume
be smooth and projective, and assume
![]() (e.g. a Fano variety). The Cox ring
(e.g. a Fano variety). The Cox ring
![]() is
is
![]() where:
where:
Remark.
The Hilbert function
![]() if
if ![]() has no higher cohomology, so is a `polynomial in
has no higher cohomology, so is a `polynomial in ![]() '. For example, if
'. For example, if
![]() ample cone
ample cone![]() , Kodaira vanishing implies that
, Kodaira vanishing implies that
![]() .
.
If ![]() is nef (
is nef (![]() is nef if
is nef if
![]() for every curve
for every curve ![]() ) and big (
) and big (![]() is big if
is big if ![]() is in the interior of the effective cone), for example if
is in the interior of the effective cone), for example if ![]() is Fano, then
is Fano, then
![]() for all
for all ![]() nef and big. Our basic strategy: use knowledge of the Hilbert function to read off the structure of
nef and big. Our basic strategy: use knowledge of the Hilbert function to read off the structure of
![]() . There is hope that the ring will be finitely generated from this polynomial expression.
. There is hope that the ring will be finitely generated from this polynomial expression.
Finite Generation
What are necessary conditions for
![]() to be finitely generated? (Part of a theorem of Hu, Keel which give necessary and sufficient conditions.) We must have:
to be finitely generated? (Part of a theorem of Hu, Keel which give necessary and sufficient conditions.) We must have:
There are also sufficient conditions:
![]()
Remark.
The universal torsor
![]() as an explicitly defined open subset, if
as an explicitly defined open subset, if
![]() is finitely generated.
is finitely generated.
![]() Cubic Surface
Cubic Surface
This is joint work with Tschinkel. The ![]() cubic surface
cubic surface ![]() is defined by the equation
is defined by the equation
![]() embedded in
embedded in
![]() ; it contains a unique line
; it contains a unique line
![]() , and a unique singularity
, and a unique singularity ![]() .
.
Analysis of the singularity: In affine coordinates, we have
![]() . We rewrite this as
. We rewrite this as
![]() , and up to analytic equivalence, this is
, and up to analytic equivalence, this is
![]() , which is the normal form of an
, which is the normal form of an ![]() singularity.
singularity.
The resolution
![]() has six
has six ![]() exceptional curves in an
exceptional curves in an ![]() -diagram, and
-diagram, and
![]() has intersection form
has intersection form

![$\displaystyle \xymatrix{
& & 2 \ar@{-}[d] \\
1 \ar@{-}[r] & 3 \ar@{-}[r] & 6 \ar@{-}[r] & 5 \ar@{-}[r] & 4 \ar@{-}[r] & \ell.
}$](img53.gif)
The inverse of this matrix is given by

The inverse proves that:
Proposition. The effective cone of ![]() is generated by
is generated by
![]() ; the nef cone is generated by
; the nef cone is generated by ![]() .
.
We have
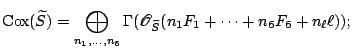
We have
![]() , but this is not surjective. We need additional generators. We let
, but this is not surjective. We need additional generators. We let
![]() ; since
; since ![]() is semiample, we have
is semiample, we have
![]() by Riemann-Roch, and
by Riemann-Roch, and
![]() is a conic bundle. Then
is a conic bundle. Then
Fact.
We have a surjection
![]() .
.
Now we look for relations among these generators. By the Hilbert function, we know that
![]() , but we have
, but we have ![]() elements of degree
elements of degree
![]() in the polynomial ring:
in the polynomial ring:
Since
![]() ,
,
![]() ,
,
![]() ,
,
![]() after renormalization, so the original equation
after renormalization, so the original equation
![]() gives the relation
gives the relation
This method should also work for other very singular cubic surfaces.
Back to the
main index
for Rational and integral points on higher dimensional varieties.