Vojta: Big semistable vector bundles

Bigness

Throughout this talk, $k$ is a field of characteristic zero, algebraically closed unless otherwise specified.

A variety is an integral scheme, separated and of finite type over a field.

Throughout this talk, $X$ is a complete variety over $k$.

Definition: Let $\mathcal L$ be a line sheaf on $X$. We say that $\mathcal L$ is big if there is a constant $c>0$ such that $h^0(X,\mathcal L^{\otimes n})\ge cn^{\dim X}$ for all sufficiently large and divisible $n\in\mathbb{Z}$.

Lemma. (Kodaira) Let $\mathcal L$ be a line sheaf and $\mathcal A$ an ample line sheaf on $X$. Then $\mathcal L$ is big iff $\mathcal L^{\otimes n}\otimes\mathcal A\spcheck$ has a (nonzero) global section for some $n>0$.

Proof: `` $\impliedby$'' is obvious.

``$\implies$'': Write $\mathcal A\cong\mathcal O(A_1-A_2)$ with $A_1$ a reduced effective very ample divisor. It will suffice to show that $\mathcal L^{\otimes n}(-A_1)$ has a global section for some $n>0$. Consider the exact sequence

$$0 \to H^0(X,\mathcal L^{\otimes n}(-A_1)) \to H^0(X,\mathcal L^{\otimes n}) \to H^0(A_1,\mathcal L^{\otimes n})\;.$$

The middle term has rank $\gg n^{\dim X}$, but the rightmost term has rank $\ll n^{\dim X-1}$, for $n\gg0$ divisible.$\qedsymbol$

Definition: A vector sheaf $\mathcal E$ of rank $r$ on $X$ is big if there is a $c>0$ such that

$$h^0(X,S^n\mathcal E)\ge cn^{\dim X+r-1}$$

for all $n\gg0$ divisible.

Equivalently, $\mathcal E$ is big iff $\mathcal O(1)$ on $\mathbb{P}(\mathcal E)$ is big.

Essential base locus

Definition: Assume that $X$ is projective, and let $\mathcal L$ be a (big) line sheaf on $X$. The essential base locus of $\mathcal L$ is the subset

$$\bigcap_{n\in\mathbb{Z}_{>0}} \hbox{(base locus of } \mathcal L^{\otimes n}(-A))$$

for any ample divisor $A$ on $X$ (it is independent of $A$). The essential base locus of a vector sheaf $\mathcal E$ on $X$ is the set $\pi(E)$, where $E$ is the essential base locus of $\mathcal O(1)$ on $\mathbb{P}(\mathcal E)$ and $\pi\:\mathbb{P}(\mathcal E)\to X$ is the canonical morphism.

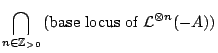
Question: If $\mathcal E$ is a big vector sheaf, is its essential base locus properly contained in $X$?

Answer: No. Example: Unstable $\mathcal E$ over curves.

Question: What if $\mathcal E$ is big and semistable?

Curves

Throughout this section, $X$ is a (projective) curve.

Definition: (Mumford) A vector sheaf $\mathcal E$ on $X$ is semistable if, for all short exact sequences

$$0 \to \mathcal E' \to \mathcal E \to \mathcal E'' \to 0$$

of nontrivial vector sheaves on $X$,

$$\frac{\deg\mathcal E'}{{\mathrm{rk}}\mathcal E'} \le \frac{\deg\mathcal E}{{\mathrm{rk}}\mathcal E}$$

or (equivalently)

$$\frac{\deg\mathcal E''}{{\mathrm{rk}}\mathcal E''} \ge \frac{\deg\mathcal E}{{\mathrm{rk}}\mathcal E}\;.$$

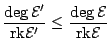
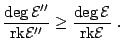
Theorem. Let $\mathcal E$ be a big semistable vector sheaf on $X$. Then $\mathcal E$ is ample (i.e., $\mathcal O(1)$ is ample on $\mathbb{P}(\mathcal E)$). In particular, the essential base locus of $\mathcal E$ is empty.

Proof: By Kleiman's criterion for ampleness, the sum of an ample and a nef divisor is again ample, so by Kodaira's lemma it suffices to show that if $\mathcal E$ is a semistable vector sheaf on $X$, then all effective divisors $D$ on $\mathbb{P}(\mathcal E)$ are nef.

So, let $D$ be an effective divisor and $C$ a curve on $\mathbb{P}(\mathcal E)$. We want to show:

$$(D\idot C)\ge0\;.$$

Since $\mathcal E$ is semistable, so is $\bigl(\pi \big\vert _C\bigr)^{*}\mathcal E$ (proof later).

Therefore we may assume that $C$ is a section of $\pi$, and that $D$ is a prime divisor.

Since $C$ is a section, it corresponds to a surjection $\mathcal E\to\mathcal L\to 0$. Moreover, $\mathcal L\cong\mathcal O(1)\big\vert _C$. By semistability, therefore,

$$(\mathcal O(1)\idot C)\ge\frac{\deg\mathcal E}{{\mathrm{rk}}\mathcal E}\;. \phantom{XXXXXXXXXXXXXXXXXXX}(*)$$

Now consider $D$. Let $d$ be the degree of $D$ on fibers of $\pi$; $d>0$. Then $\mathcal O(D)\cong\mathcal O(d)\otimes\pi^{*}\mathcal M$ for some $\mathcal M\in{\mathrm{Pic}}X$. Thus $D$ corresponds to a section of $\mathcal M\otimes S^d\mathcal E$, hence we have an injection

$$0 \to \mathcal O_X \to \mathcal M\otimes S^d\mathcal E$$

with locally free quotient.

Since $\mathcal E$ is semistable, so is $S^d\mathcal E$ (proof later); hence

$$\deg(\mathcal M\otimes S^d\mathcal E)\ge0\; \phantom{XXXXXXXXXXXXXXXXXXX}(**)$$

Let $r={\mathrm{rk}}\mathcal E$; then $S^d\mathcal E$ has rank $r':=\binom{r+d-1}{d}$. The diagram

$$\xymatrix{ GL_r(k) {\ar[r]} \ar[d] & GL_{r'}(k) \ar[d] \\ k^{*} \ar[r] & k^{*} }$$

commutes for all diagonal matrices, hence for all diagonalizable matrices, hence for all matrices. Thus

$$\deg(\mathcal M\otimes S^d\mathcal E) = r'\deg\mathcal M + \binom{r+d-1}{d-1}\deg\mathcal E \cr$$

and therefore by (**),

$$\deg\mathcal M \ge -\frac dr\deg\mathcal E\;.$$

Thus by (*),

$$(D\idot C) = d(\mathcal O(1)\idot C) + \deg\mathcal M \ge \frac dr\deg\mathcal E-\frac dr\deg\mathcal E \ge 0\;.\qed$$

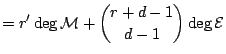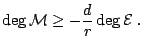
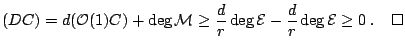
Higher Dimensional Varieties

Let $X$ again be a complete variety of arbitrary dimension.

Construction: Given a vector sheaf $\mathcal E$ on $X$ of rank $r$ and a representation

$$\rho: GL_r(k)\to GL_{r'}(k)\;,$$

we can construct a vector sheaf $\mathcal E^{(\rho)}$ on $X$ of rank $r'$ by applying $\rho$ to the transition matrices of $\mathcal E$. Equivalently, if $\mathcal E$ corresponds to $\xi\in H^1(X, GL_r(\mathcal O_X))$, then $\rho(\xi)\in H^1(X, GL_{r'}(\mathcal O_X))$ corresponds to $\mathcal E^{(\rho)}$.

Examples of this include $S^d$, $\det$, and $\wedge^d$.

Definition: (Bogomolov) A vector sheaf $\mathcal E$ of rank $r$ on $X$ is unstable if there exists a representation $\rho\:GL_r(k)\to GL_{r'}(k)$ of determinant 1 (i.e., factoring through $PGL_r(k)$) such that $\mathcal E^{(\rho)}$ has a nonzero section that vanishes at at least one point. It is semistable if it is not unstable.

Theorem. (Bogomolov) If $X$ is a curve, then Bogomolov's definition of semistability agrees with Mumford's.

Remark: If $\rho$ has determinant $1$ then $Im\,\rho\subseteq SL_{r'}(k)$, but not conversely.

Indeed, the representation $GL_1(k)\to GL_2(k)$, $z\mapsto\pmatrix z&0\\ 0&z^{-1}\endpmatrix$, has image contained in $SL_2(k)$ but its does not factor through $PGL_1(k)$.

To see that the (true) converse holds, first show that the vanishing of the determinant defines an irreducible subset of $k^{r^2}$; this is left as an exercise for the reader. Now suppose that $\rho\:GL_r(k)\to GL_{r'}(k)$ is a representation that factors through $PGL_r(k)$, and suppose also that its image is not contained in $SL_{r'}(k)$. Then $\det\circ\rho$ is a nonconstant regular function $PGL_r(k)\to k^{*}$, hence it determines a nonconstant rational function on $\mathbb{P}^{r^2}_k$ with zeros and poles contained in $\{\det=0\}$. But the latter is irreducible, so it can't have both zeroes and poles there, contradiction.

So now we can pose:

Question: If $X$ is a projective variety and $\mathcal E$ is a big, semistable vector sheaf on $X$, then is the essential base locus of $\mathcal E$ a proper subset of $X$?

Remark: We can't conclude that $\mathcal E$ is ample in the above, as the following example illustrates. Let $X$ be a projective variety of dimension $>1$, let $\mathcal E$ be a big semistable vector sheaf on $X$ of rank $>1$, let $\pi\:X'\to X$ be the blowing-up of $X$ at a closed point, and let $F$ be the exceptional divisor. Then the essential base locus of $\pi^{*}\mathcal E$ must contain $F$.

My Mitteljahrentraum

The question of an essential base locus being a proper subset comes up in Nevanlinna theory, and I hope to be able to use it in number theory, as well. Here's how.

Bogomolov has shown that $\Omega^1_X$ is semistable for a smooth surface $X$. One would hope to generalize this, to $\Omega^1_X(\log D)$ for a normal crossings divisor $D$ on $X$, and also to higher dimensions. Then it would suffice to prove that one of these bundles is big to get arithmetical consequences.

Moreover, Bogomolov's definition of semistability can be generalized to defining semistability of higher jet bundles. These are not vector bundles, because they correspond to elements of $H^1(X,G(\mathcal O_X))$ for a group $G$ other than $GL_n$. But, one can make the same definition, using those representations of $G$ having the appropriate kernel: $k^{*}$ again (Green-Griffiths), or a certain bigger group (Semple-Demailly). Probably the latter.

Bigness is easy to define in this context, and then one hopefully can use the two properties to talk about the exceptional base locus. Already the proof of Bloch's theorem in Nevanlinna theory can probably be recast in this mold.

Is Semistability Really Necessary?

The proof of the main theorem of this talk didn't really need the full definition of semistability; it only used the condition on the degrees of subbundles for subbundles of rank 1 and corank 1. Would the following definition make sense, and would it be preserved under pull-back and symmetric power?

Definition: Let $X$ be a projective curve and let $\mathcal E$ be a vector sheaf of rank $r$ on $X$. Then $\mathcal E$ is $\pm1$-semistable if the condition on degrees and ranks of subbundles holds for all full subbundles $\mathcal E'$ of rank $1$ and corank $1$.

Again, what would be a reasonable representation-theoretic formulation of this definition?

Loose Ends

In the proof of the main theorem it remains to show that semistability is preserved under pull-back and under taking $S^d$.

To show the first assertion, let $f\:X'\to X$ be generically finite, and let $\mathcal E$ be a semistable vector sheaf on $X$. Suppose that $f^{*}\mathcal E$ is unstable. Let $\rho\: GL_r(k)\to GL(V)$ be a representation such that $(f^{*}\mathcal E)^{(\rho)}$ has a nonzero global section that vanishes somewhere. Let $d=\deg f$. Then taking norms gives a global section of

$$S^d(\mathcal E^{(\rho)})=\mathcal E^{(S^d\circ\rho)}$$

with the same properties, contradiction.

The second assertion is proved similarly: suppose there is a representation

$$\rho\: GL(S^d(k^r))\to GL(V)$$

with the required properties. Then $\rho\circ S^d$ gives a representation $GL_r\to GL(V)$, leading to a contradiction as before. It only remains to check that $\rho\circ S^d$ has determinant $1$. This follows by commutativity of the following diagram:

$$\xymatrix{ GL_r(k) {\ar[r]} \ar[d] & GL_{r'}(k) \ar[d] \\ PGL_r(k) \ar[r] & PGL_{r'}(k) }$$

(here $r'$ is the rank of $S^d\mathcal E$).

Back to the main index for Rational and integral points on higher dimensional varieties.

ARRAY(0x8ddb63c)