We consider the following problem: Given a prime ![]() and
and
![]() , where
, where ![]() ,
, ![]() is separable, and
is separable, and ![]() splits completely, find a proper factor of
splits completely, find a proper factor of ![]() (in deterministic polynomial time).
(in deterministic polynomial time).
Berlekamp algorithm reduces general polynomials in
![]() (
(![]() a power of
a power of ![]() ) to polynomials of the above type. Without GRH, we are stuck already at
) to polynomials of the above type. Without GRH, we are stuck already at ![]() . So throughout we assume GRH.
. So throughout we assume GRH.
Ronyai (1988) shows that this can be done in time
![]() , or more precisely
, or more precisely
![]() whenever
whenever ![]() ,
, ![]() , so in particular if
, so in particular if ![]() is even
is even ![]() can be split in deterministic polynomial time. Bach, von zur Gathen and Lenstra (2001) give an algorithm with polynomial time if
can be split in deterministic polynomial time. Bach, von zur Gathen and Lenstra (2001) give an algorithm with polynomial time if ![]() is smooth for some
is smooth for some ![]() where
where ![]() is the
is the ![]() th cyclotomic polynomial. Evdokimov (1994) shows for any
th cyclotomic polynomial. Evdokimov (1994) shows for any ![]() and
and ![]() ,
, ![]() can be factored in time
can be factored in time
![]() . We discuss work in Cheng and Huang (2000), and Gao (2001) plus some unpublished results. GRH will be needed only to compute an
. We discuss work in Cheng and Huang (2000), and Gao (2001) plus some unpublished results. GRH will be needed only to compute an ![]() th nonresidue in
th nonresidue in
![]() or in its extensions, for
or in its extensions, for
![]() .
.
Definition.
An algebra
![]() is called elementary if
is called elementary if
![]() for some
for some ![]() .
.
Let ![]() be elementary over
be elementary over
![]() . Then we write
. Then we write
![]() where the
where the
![]() are primitive idempotents, which are unique in
are primitive idempotents, which are unique in ![]() .
.
Fact.
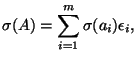
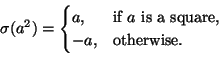
Now let
![]() be separable, so that
be separable, so that
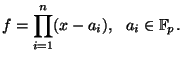
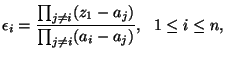
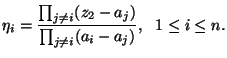
Then
![]() ,
,
![]() , are all the primitive idempotents of
, are all the primitive idempotents of ![]() . They have the following properties:
. They have the following properties:
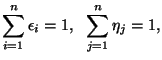
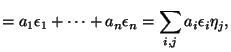 |
||
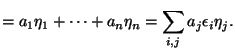 |
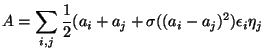
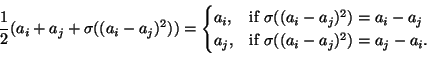
Hence ![]() encodes information about the "squareness" of the differences of the roots of
encodes information about the "squareness" of the differences of the roots of ![]() . By using characteristic polynomials and gcd technique, one can extract the factors of
. By using characteristic polynomials and gcd technique, one can extract the factors of ![]() .
.
Definition.
For
![]() , define
, define
Theorem. We can always find a proper factor of ![]() in
in
![]() except when
except when
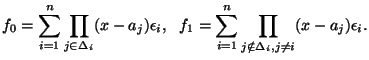
To further factor ![]() over
over
![]() , we compute in the ring
, we compute in the ring
A system of subsets satisfying (![]() ) and (
) and (![]() ) is called
an Hadamard design. When
) is called
an Hadamard design. When
![]() is a prime, there is always
an Hadamard design.
is a prime, there is always
an Hadamard design.
To further split ![]() , let
, let
![]() , and we compute
in the ring
, and we compute
in the ring
Back to the
main index
for Future directions in algorithmic number theory.