Disclaimer: These are rough notes only, aimed at setting the scene and
promoting discussion at the American Institute of Mathematics Research
Conference Center Workshop `Conformal Structure in Geometry,
Analysis, and Physics,'
![]() -
-
![]() August 2003.
For simplicity, we have omitted all references. Curvature conventions are in an
appendix. Conversations with Tom Branson and Rod Gover have been extremely
useful.
August 2003.
For simplicity, we have omitted all references. Curvature conventions are in an
appendix. Conversations with Tom Branson and Rod Gover have been extremely
useful.
Let ![]() be an oriented even-dimensional Riemannian
be an oriented even-dimensional Riemannian ![]() -manifold. Branson's
-manifold. Branson's
![]() -curvature is a canonically defined
-curvature is a canonically defined ![]() -form on
-form on ![]() . It is not conformally
invariant but enjoys certain natural properties with respect to conformal
transformations.
. It is not conformally
invariant but enjoys certain natural properties with respect to conformal
transformations.
When ![]() , the
, the ![]() -curvature is a multiple of the scalar curvature. With
conventions as in the appendix
-curvature is a multiple of the scalar curvature. With
conventions as in the appendix ![]() . Under conformal rescaling of the
metric,
. Under conformal rescaling of the
metric,
![]() we have
we have
When ![]() , the
, the ![]() -curvature is given by
-curvature is given by
For general even ![]() , the
, the ![]() -curvature transforms as follows:-
-curvature transforms as follows:-
Even when ![]() is conformally flat, the existence of
is conformally flat, the existence of ![]() is quite subtle. We can
reason as follows. When
is quite subtle. We can
reason as follows. When ![]() is actually flat then
is actually flat then ![]() must vanish. Therefore,
in the conformally flat case, locally if we write
must vanish. Therefore,
in the conformally flat case, locally if we write
![]() where
where ![]() is flat, then (
is flat, then (![]() ) implies that
) implies that
That ![]() is conformally invariant on flat space is well-known. It
may also be verified directly by a rather similar calculation. For example,
here is the calculation when
is conformally invariant on flat space is well-known. It
may also be verified directly by a rather similar calculation. For example,
here is the calculation when ![]() . For general conformally related metrics
. For general conformally related metrics
![]() in dimension 4,
in dimension 4,
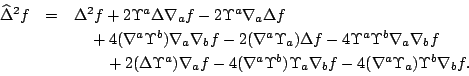
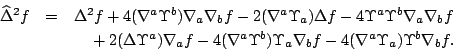
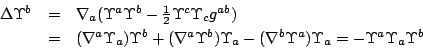
Conundrum: Deduce fact 2 from fact 1 or vice versa. Both are consequences
of (![]() ). Alternatively, construct a Lie algebraic proof of fact 2. There is a Lie algebraic proof of fact 1. It corresponds to the
existence of a homomorphism between certain generalised Verma modules for
). Alternatively, construct a Lie algebraic proof of fact 2. There is a Lie algebraic proof of fact 1. It corresponds to the
existence of a homomorphism between certain generalised Verma modules for
![]() .
.
What about a formula for ![]() , even in the conformally flat case? We have a
recipe for
, even in the conformally flat case? We have a
recipe for ![]() , namely (
, namely (![]() ), but it is not a formula. We may
proceed as follows.
), but it is not a formula. We may
proceed as follows.
If
![]() and
and ![]() is flat, then
(
is flat, then
(![]() ) implies that
) implies that
To proceed further we need two identities. If ![]() has conformal weight
has conformal weight ![]() ,
then as described in the appendix,
,
then as described in the appendix,
The quantities in (![]() ) have weight
) have weight ![]() . Therefore, applying
(
. Therefore, applying
(![]() ) gives
) gives
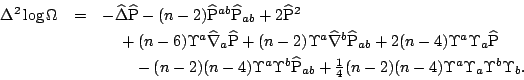
Of course, we may continue in the vein, further differentiating (![]() ) to
obtain a formula for
) to
obtain a formula for
![]() expressed in terms of complete
contractions of
expressed in terms of complete
contractions of
![]() , its hatted derivatives, and
, its hatted derivatives, and ![]() .
With increasing
.
With increasing ![]() , this gets rapidly out of hand. Moreover, it is only
guaranteed to give
, this gets rapidly out of hand. Moreover, it is only
guaranteed to give ![]() in the conformally flat case. Indeed, when
in the conformally flat case. Indeed, when ![]() this
naive derivation of
this
naive derivation of ![]() fails for a general metric. Nevertheless, there
are already some questions in the conformally flat case.
fails for a general metric. Nevertheless, there
are already some questions in the conformally flat case.
Conundrum: Find a formula for ![]() in the conformally flat case. Show that the
procedure outlined above produces a formula for
in the conformally flat case. Show that the
procedure outlined above produces a formula for ![]() .
.
In fact, there is a tractor formula for the conformally flat ![]() . This is not
the place to explain the tractor calculus but, for those who know it already:-
. This is not
the place to explain the tractor calculus but, for those who know it already:-
![\begin{displaymath}\square\left[\begin{array}cn-2\\ 0\\ -\mathrm{P}\end{array}\right]=
\left[\begin{array}c0\\ 0\\ Q\end{array}\right]\end{displaymath}](img73.gif)
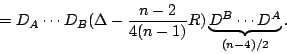
Recall that, like ![]() , the Pfaffian is an
, the Pfaffian is an ![]() -form canonically associated to a
Riemannian metric on an oriented manifold in even dimensions. It is defined as
a complete contraction of
-form canonically associated to a
Riemannian metric on an oriented manifold in even dimensions. It is defined as
a complete contraction of ![]() copies of the Riemann tensor with two copies of
the volume form. For example, in dimension four it is
copies of the Riemann tensor with two copies of
the volume form. For example, in dimension four it is
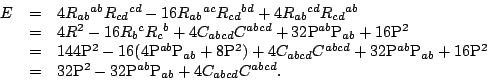
Conundrum: Find a direct link between ![]() and the Pfaffian in the conformally flat
case. Prove directly that
and the Pfaffian in the conformally flat
case. Prove directly that ![]() is a topological invariant in this case.
is a topological invariant in this case.
Conundrum: Is it true that, on a general Riemannian manifold, ![]() may be written as a
multiple of the Pfaffian plus a local conformal invariant plus a divergence?
may be written as a
multiple of the Pfaffian plus a local conformal invariant plus a divergence?
Recall the conventions for Weyl structures as in the appendix. In particular, a
metric in the conformal class determines a ![]() -form
-form ![]() . In fact, a
Weyl structure may be regarded as a pair
. In fact, a
Weyl structure may be regarded as a pair
![]() subject to
equivalence under the simultaneous replacements
subject to
equivalence under the simultaneous replacements
structure as follows. Since ![]() is a Riemannian invariant, the differential
operator
is a Riemannian invariant, the differential
operator ![]() is necessarily of the form
is necessarily of the form
![]() for some
Riemannian invariant linear differential operator from
for some
Riemannian invariant linear differential operator from ![]() -forms to
-forms to ![]() -forms.
Now, if
-forms.
Now, if
![]() is a Weyl structure, choose a representative metric
is a Weyl structure, choose a representative metric
![]() and consider the
and consider the ![]() -form
-form
In combination with (![]() ) we obtain
) we obtain
Conundrum: Can we find such a ![]() in general even dimensions?
Presumably, this would restrict the choice of Riemannian
in general even dimensions?
Presumably, this would restrict the choice of Riemannian ![]() .
.
Though ![]() given by (
given by (![]() ) is an invariant of the Weyl
structure, it is not manifestly so. Better is to rewrite it as follows. Using
conventions from the appendix, we may write the Schouten tensor
(
) is an invariant of the Weyl
structure, it is not manifestly so. Better is to rewrite it as follows. Using
conventions from the appendix, we may write the Schouten tensor
(![]() ) of the Weyl structure in terms of the Schouten tensor of a
representative metric
) of the Weyl structure in terms of the Schouten tensor of a
representative metric ![]() :-
:-
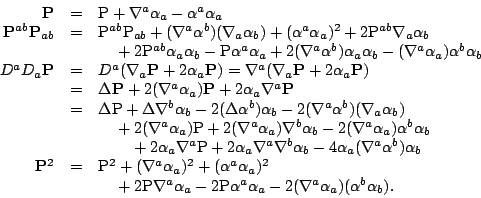
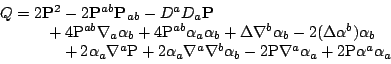
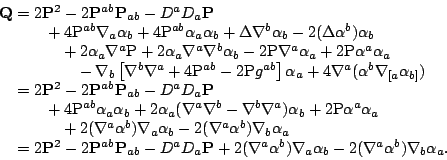
Conundrum: Did we really need to go through this detailed calculation? What are the
implications, if any, for the operator
![]() ?
?
Conundrum: Can we characterise the Riemannian ![]() by sufficiently many properties? Do
Weyl structures help in this regard?
by sufficiently many properties? Do
Weyl structures help in this regard?
Tom Branson has suggested that, for two metrics ![]() and
and
![]() in the same conformal class on a compact manifold
in the same conformal class on a compact manifold ![]() , one should consider the
quantity
, one should consider the
quantity
Conundrum: Are there any deeper properties of Branson's cocycle
![]() ?
?
One possible rôle for ![]() is in a curvature prescription problem:-
is in a curvature prescription problem:-
Conundrum: On a given manifold ![]() , can one find a metric with specified
, can one find a metric with specified ![]() ?
?
One can also ask this question within a given conformal class or within the
realm of conformally flat metrics though, of course, if ![]() is compact, then
is compact, then
![]() must be as specified by the conformal class and the topology of
must be as specified by the conformal class and the topology of ![]() .
There is also the question of uniqueness:-
.
There is also the question of uniqueness:-
Conundrum: When does ![]() determine the metric up to constant rescaling within a given
conformal class?
determine the metric up to constant rescaling within a given
conformal class?
Since we know how ![]() changes under conformal rescaling (
changes under conformal rescaling (![]() ),
this question is equivalent to
),
this question is equivalent to
Conundrum: When does the equation ![]() have only constant solutions?
have only constant solutions?
On a compact manifold in two dimensions this is always true: harmonic functions
are constant. In four dimensions, though there are conditions under which
![]() has only constant solutions, there are also counterexamples, even on
conformally flat manifolds. The following counterexample is due to Michael
Singer and the first author. Consider the metric in local coördinates
has only constant solutions, there are also counterexamples, even on
conformally flat manifolds. The following counterexample is due to Michael
Singer and the first author. Consider the metric in local coördinates
APPENDIX: Curvature Conventions
Firstly, our conventions for conformal weight. A density ![]() of conformal
weight
of conformal
weight ![]() may be identified as a function for any metric in the conformal
class. At the risk of confusion, we shall also write this function as
may be identified as a function for any metric in the conformal
class. At the risk of confusion, we shall also write this function as ![]() . If
however, our choice of metric
. If
however, our choice of metric ![]() is replaced by a conformally equivalent
is replaced by a conformally equivalent
![]() , then the function
, then the function ![]() is replaced by
is replaced by
![]() . Quantities that are not conformally invariant can still
have a conformal weight with respect to constant rescalings. For example, the
scalar curvature has weight
. Quantities that are not conformally invariant can still
have a conformal weight with respect to constant rescalings. For example, the
scalar curvature has weight ![]() in this respect. Explicit conformal
rescalings are generally suppressed.
in this respect. Explicit conformal
rescalings are generally suppressed.
The Riemann curvature is defined by
A Weyl structure is a conformal structure together with a choice of
torsion-free connection ![]() preserving the conformal structure. In other
words, if we choose a metric
preserving the conformal structure. In other
words, if we choose a metric ![]() in the conformal class, then
in the conformal class, then
where ![]() is the Levi-Civita connection for the metric
is the Levi-Civita connection for the metric ![]() . Let
. Let
![]() denote the Ricci curvature of the connection
denote the Ricci curvature of the connection ![]() :-
:-
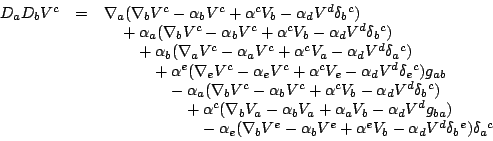
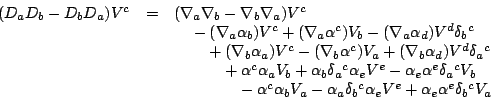
for
Back to the
main index
for Conformal structure in Geometry, Analysis, and Physics .