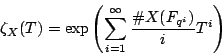Effective computation of zeta-functions
The Weil conjectures (proved by Dwork, Grothendieck, Deligne et al.)
assert that for any algebraic variety 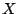 over
a finite field
over
a finite field 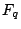 , the power series
, the power series
is a rational function of 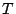 ; giving explicit methods for computing
; giving explicit methods for computing
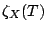 is a fundamental problem in computational number theory.
In principle, one can do this by simply giving bounds on the degrees of
the numerator and denominator, then explicitly computing
is a fundamental problem in computational number theory.
In principle, one can do this by simply giving bounds on the degrees of
the numerator and denominator, then explicitly computing
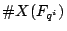 for enough values of
for enough values of 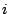 . (E.g., if
. (E.g., if 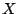 is projective, one can choose
a projective embedding of
is projective, one can choose
a projective embedding of 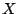 , defined by certain equations, then count the
number of points in projective space satisfying those equations.)
In practice, this enumeration gives an algorithm which requires time
exponential in
the ``complexity'' of
, defined by certain equations, then count the
number of points in projective space satisfying those equations.)
In practice, this enumeration gives an algorithm which requires time
exponential in
the ``complexity'' of 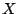 (e.g., the logarithm of the base field size
(e.g., the logarithm of the base field size 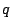 ,
and the degrees of the equations defining
,
and the degrees of the equations defining 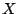 ) and thus can only be completed
for relatively small examples.
) and thus can only be completed
for relatively small examples.
Below we describe
the current state of knowledge regarding subexponential methods for
computing zeta functions.
We omit mention of methods which
improve on pure exhaustion but are still exponential, such as Mestre's
``baby step-giant step'' method for computing the zeta function of an
elliptic curve.
Back to the
main index
for L-functions and Random Matrix Theory.
![]() over
a finite field
over
a finite field ![]() , the power series
, the power series