Long Mollifiers

Let $h(x)$ be a real polynomial with $h(0)=0$, let $y=T^\theta$ for some $\theta>0$, and let

$$M(s)= M(s, h(x)) =\sum_{n\le y} \frac{\mu(n)\,h\left( {\frac{\log y/n}{\log y}}\right)}{n^s}.$$

The Dirichlet polynomial $M(s)$ is called a ``mollifier'' of the Riemann $\zeta$-function because it is an approximation to $1/\zeta(s)$, and so $\zeta(s)M(s)$ should be much better behaved than $\zeta(s)$ near the $\frac12$-line.

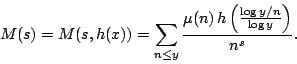
The mean value of $\zeta(s)M(s)$ near the $\frac12$-line is a fundamental tools for studying zeros of the $\zeta$-function. The most general version currently used is the following formula of Conrey, Ghosh, and Gonek [ MR 90h:11077]

$$\begin{eqnarray*} \int_1^T &&\,\zeta(\frac12+u+it)\,\zeta(\frac12+v-it)\,M(\fra... ...(x+\alpha)g_b(x+\beta)\,dx\right)\Biggl\vert _{\alpha=\beta=0} , \end{eqnarray*}$$

where $h_a(x)=T^{\theta a(x-1)}h(x)$, uniformly for $\vert u\vert+\vert v\vert+\vert a\vert+\vert b\vert\ll 1/\log T$. This formula is used in Levinson's method [ MR 58 #27837], and is known to be valid [ MR 90g:11120] for $0<\theta<\frac47$. Showing that the formula is valid for large $\theta$ is key to having good results.

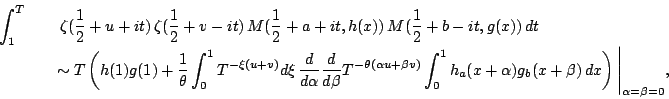
Farmer [ MR 95a:11076] conjectured that the above formula should remain valid for all $\theta>0$. This leads to a conjecture for an integral involving ratios of zeta-functions, which implies the pair-correlation conjecture. See the original paper [ MR 95a:11076] for some additional consequences.

It would be a significant result to prove that the above formula holds for some $\theta>\frac47$. Establishing it for $\theta>0.7631$ would prove that more than half of the zeros of the $\zeta$-function are on the $\frac12$-line. Proving that it holds for all $\theta>0$ is more-or-less equivalent to the GUE conjecture, because it can be deduced from the formulas for ratios of zeta-functions.

Back to the main index for L-functions and Random Matrix Theory.