Moments of $S(T)$
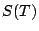 is defined by
is defined by
where the argument is obtained by continuous variation from 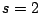 where the argument is 0, to
where the argument is 0, to 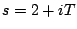 to
to 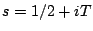 , circumventing zeros of
, circumventing zeros of 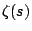 by small semicircular detours above the zeros. Selberg
[
MR 8,567e] proved an asymptotic formula for
by small semicircular detours above the zeros. Selberg
[
MR 8,567e] proved an asymptotic formula for
for positive integral values of 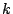 and an appropriate
and an appropriate 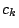 .
Goldston [
MR 89a:11086], assuming the Riemann Hypothesis, was able to give a second main term in the case that
.
Goldston [
MR 89a:11086], assuming the Riemann Hypothesis, was able to give a second main term in the case that 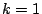 . Keating and Snaith's conjectures for moments of
. Keating and Snaith's conjectures for moments of
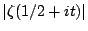 imply
formula for the above moments of
imply
formula for the above moments of 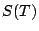 , including lower order terms all the way to a constant, i.e. they conjecture that
, including lower order terms all the way to a constant, i.e. they conjecture that
for some explicit constants 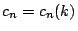 .
.
It seems like further work should allow one to obtain the lower order terms in the moments of 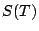 ; it's possible that the assumption of the Riemann Hypothesis will allow for the evaluation of some of the lower order terms, and the assumption of GUE will allow for the rest.
; it's possible that the assumption of the Riemann Hypothesis will allow for the evaluation of some of the lower order terms, and the assumption of GUE will allow for the rest.
Back to the
main index
for L-functions and Random Matrix Theory.
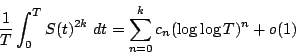
![]() ; it's possible that the assumption of the Riemann Hypothesis will allow for the evaluation of some of the lower order terms, and the assumption of GUE will allow for the rest.
; it's possible that the assumption of the Riemann Hypothesis will allow for the evaluation of some of the lower order terms, and the assumption of GUE will allow for the rest.