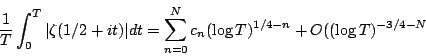Fractional moments

There is now a preliminary conjecture for the lower order terms of the above article in the case of integral moments. However, it would be interesting to have the lower order terms for fractional moments as well. For example, we expect that

$$\frac{1}{T} \int_0^T\vert\zeta(1/2+it)\vert~dt \sim c (\log T)^{1/4}.$$

What would be the expected error term here? Are there more main terms? It may not be unreasonable to guess that for this example there will be an (infinite) asymptotic series of powers of 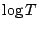$\log T$ so that

$$\frac{1}{T} \int_0^T\vert\zeta(1/2+it)\vert dt= \sum_{n=0}^N c_n (\log T)^{1/4-n} +O((\log T)^{-3/4-N}$$

holds for any 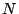$N$ with some sequence of 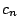$c_n$. Is there some way to guess this answer? A good conjecture could easily be tested numerically.

Back to the main index for L-functions and Random Matrix Theory.