Partial Differential Equations and Numerical Methods

By replacing the constraint that the measure 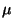$\mu$ is a generalized curve by

$$\int v D_x\phi(x) +\epsilon \Delta\phi(x)d\mu,$$

which corresponds to a generalized diffusion, the dual problem is now related to a second-order Hamilton-Jacobi equation [Gomes4]

$$-\epsilon \Delta u+H(D_xu,x)=\Hh.$$

Using these new minimizing measures one can prove regularity results for second derivatives of the solution 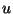$u$ which do not depend on the parameter 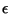$\epsilon$, for instance

$$\int \vert D^2_{xx}u\vert^2\leq C,$$

uniformly in 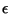$\epsilon$.

Furthermore, the duality methods yield a representation formula for $\Hh$ which can be used in numerical computations [GomesOberman1], Some of the problems that deserve further research are:

1. Regularity for partial differential equations, namely non- strictly convex Hamilton-Jacobi
2. Generalization to fully-nonlinear equations
3. Numerical computation of the solution 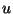$u$ and $\Hh$ [Qian], [GomesOberman1].

Gom02b

BB00

Jean-David Benamou and Yann Brenier.
A computational fluid mechanics solution to the Monge-Kantorovich mass transfer problem.
Numer. Math., 84(3):375-393, 2000.

BBG02

J.-D. Benamou, Y. Brenier, and K. Guittet.
The Monge-Kantorovitch mass transfer and its computational fluid mechanics formulation.
Internat. J. Numer. Methods Fluids, 40(1-2):21-30, 2002.
ICFD Conference on Numerical Methods for Fluid Dynamics (Oxford, 2001).

Bre99

Yann Brenier.
Minimal geodesics on groups of volume-preserving maps and generalized solutions of the Euler equations.
Comm. Pure Appl. Math., 52(4):411-452, 1999.

E99

Weinan E.
Aubry-Mather theory and periodic solutions of the forced Burgers equation.
Comm. Pure Appl. Math., 52(7):811-828, 1999.

EG01

L. C. Evans and D. Gomes.
Effective Hamiltonians and averaging for Hamiltonian dynamics. I.
Arch. Ration. Mech. Anal., 157(1):1-33, 2001.

EG02a

L. C. Evans and D. Gomes.
Effective Hamiltonians and averaging for Hamiltonian dynamics II.
Arch. Ration. Mech. Anal., http://dx.doi.org/10.1007/s002050100181, 2002.

EG02b

L. C. Evans and D. Gomes.
Linear programming interpretations of Mather's variational principle.
Preprint, 2002.

Eva99

Lawrence C. Evans.
Partial differential equations and Monge-Kantorovich mass transfer.
In Current developments in mathematics, 1997 (Cambridge, MA), pages 65-126. Int. Press, Boston, MA, 1999.

Fat97a

Albert Fathi.
Solutions KAM faibles conjuguées et barrières de Peierls.
C. R. Acad. Sci. Paris Sér. I Math., 325(6):649-652, 1997.

Fat97b

Albert Fathi.
Théorème KAM faible et théorie de Mather sur les systèmes lagrangiens.
C. R. Acad. Sci. Paris Sér. I Math., 324(9):1043-1046, 1997.

Fat98a

Albert Fathi.
Orbite hétéroclines et ensemble de Peierls.
C. R. Acad. Sci. Paris Sér. I Math., 326:1213-1216, 1998.

Fat98b

Albert Fathi.
Sur la convergence du semi-groupe de Lax-Oleinik.
C. R. Acad. Sci. Paris Sér. I Math., 327:267-270, 1998.

GO02a

D. Gomes and A. Oberman.
Computational methods for effective Hamiltonians.
Preprint, 2002.

GO02b

D. Gomes and A. Oberman.
Converse KAM theory.
In preparation, 2002.

Gom02a

D. Gomes.
Perturbation theory for viscosity solutions of Hamilton-Jacobi equations and stability of Aubry-Mather sets.
Preprint, 2002.

Gom02b

D. Gomes.
Regularity theory for Hamilton-Jacobi equations.
to appear in Journal of Differential Equations, 2002.

Gom02c

D. Gomes.
A stochastic analog of Aubry-Mather theory.
Nonlinearity, 2002.

Mat91

John N. Mather.
Action minimizing invariant measures for positive definite Lagrangian systems.
Math. Z., 207(2):169-207, 1991.

Qia02

Jianliang Qian.
A simple numerical method for computing effective hamiltonians.
Preprints, 2002.

Xia98

Zhihong Xia.
Arnold diffusion: a variational construction.
In Proceedings of the International Congress of Mathematicians, Vol. II (Berlin, 1998), number Extra Vol. II, pages 867-877 (electronic), 1998.

Back to the main index for New connections between dynamical systems and PDE's.