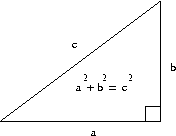Right triangles and elliptic curves

Congruent numbers naturally lead to one of the main topics of modern number theory research: elliptic curves.

Recall that the Pythagorean theorem says that if a, b, and c are the sides of a right triangle, with c the hypotenuse, then a2+b2= c2. Ancient Greek mathematicians found it interesting that it is possible for all three sides of a right triangle to be whole numbers. These are know as Pythagorean triples, and a few examples are (3,4,5), (5,12,13), (8, 15, 17), and (16, 63, 65).

It is possible to describe all Pythagorean triples by a formula. Suppose a=m2-n2, b=2mn and c=m2+n2, with m and n positive integers with m > n. Then (a,b,c) is a Pythagorean triple, and all Pythagorean triples arise in this way. The proof of that statement requires two steps. The easy direction is doing the algebra to show that (a,b,c) is a Pythagorean triple. The harder direction is showing that all Pythagorean triple arise in this way. There are several ways to do this, such as rearranging the equation to say a2=c2-b2 and then factoring both sides. 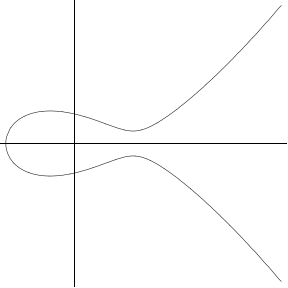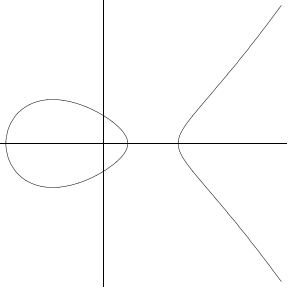Elliptic curves The connection with elliptic curves comes when we also require that the area of the triangle is an integer. But first we explain what is an elliptic curve. There are many good introductions to elliptic curves, such as Silverman and Tate's Rational Points on Elliptic Curves, or Koblitz' slightly more advanced book (which has an extensive discussion about congruent numbers) Introduction to Elliptic Curves and Modular Forms. For our purposes we give an algebraic description which unfortunately hides the beauty and depth of the subject. An elliptic curve is an equation in two parameters which can be rearranged (possibly after a change of variables) to be in the form (1)           y 2 = x3+A x + B, where A and B are rational numbers. Technical note: An equivalent definition is y2= p(x), where p(x) is a polynomial of degree 3 or 4. The change of variables y = y' + α x2 shows that if the polynomial p(x) has degree 4, then it can be replaced by a polynomial of degree 3. Then another changes of variables will eliminate the x2 term, leaving an equation of the form (1). It is also required that the curve not be singular, which in form (1) says that 4A3-27B2 is not equal to 0. Details in any book on elliptic curves. Equation (1) is easy to understand of we think of x and y as real numbers: the real solutions to the equation look like one of the following graphs:                       Things get interesting, and it becomes a number theory problem, if we instead look only for rational solutions to equation (1). Depending on A and B, the equation might have no rational solutions, or just a few, or infinitely many. A particular case concerns congruent numbers. The congruent number curve Suppose we have a right triangle with sides a, b, c so that a2+b2= c2, and its area is n = a b/2. If we let x = (c/2)2           and           y=(b2 - a2)c/8, then a little algebra finds that y2 = x3- n2 x. Furthermore (this is a simple but important point), if a, b, and c are rational numbers, then so are x and y, and y is not 0. (If y = 0, then either c = 0 and we don't actually have a triangle, or b2 = a2 in which case a = c /√2, so either a or c is irrational.) Thus, if n is a congruent number, then the elliptic curve y2 = x3- n2 x has a rational point where y is not 0. It follows that such a point must have infinite order, which is why the congruent number problem has a connection to the Birch and Swinnerton-Dyer conjecture.