A mollification problem

Baez-Duarte [ arXiv:math.NT/0202141] has recently proven that the Riemann Hypothesis is equivalent to the assertion that

$$\inf_{A_N(s)}\int_{-\infty}^\infty \vert 1-A_N(1/2+it)\zeta(1/2+it\vert^2)~\frac {dt}{\frac 14 +t^2}$$

tends to 0 as $N\to \infty$ where $A_N(s)$ can be any Dirichlet polynomial of length $N$:

$$A_N(s)=\sum_{n=1}^N \frac {a_n}{n^s}.$$

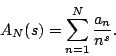
Previously, Baez-Duarte, Balazard, Landreaux, and Saias had noted that as a consequence of the Nyman-Beurling criterion, the above assertion implies RH.

Back to the main index for The Riemann Hypothesis.