Weil's positivity criterion

André Weil [ MR 14,727e] proved the following explicit formula (see also A. P. Guinand [ MR 10,104g] which specifically illustrates the dependence between primes and zeros. Let $h$ be an even function which is holomorphic in the strip $\vert\Im t\vert\le 1/2+\delta$ and satisfying $h(t)=O((1+\vert t\vert)^{-2-\delta})$ for some $\delta>0$, and let

$$g(u)=\frac{1}{2\pi}\int_{-\infty}^\infty h(r)e^{-i u r}~dr.$$

Then we have the following duality between primes and zeros:

$$\sum_{\gamma}h(\gamma)=2h(\tfrac{i}2) -g(0) \log \pi +\frac{... ... r)~dr-2\sum_{n=1}^\infty \frac{\Lambda(n)}{\sqrt{n}}g(\log n).$$

In this formula, a zero is written as $\rho=1/2+i\gamma$ where $\gamma\in \mathbb C$; of course RH is the assertion that all of the $\gamma$ are real. Using this duality Weil gave a criterion for RH.

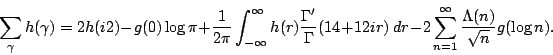
Back to the main index for The Riemann Hypothesis.