Zeros of Dirichlet polynomials

Turan showed that if for all sufficiently large $N$, the $N$th partial sum of $\zeta(s)$ does not vanish in $\sigma>1$ then the Riemann Hypothesis follows.

He [ MR 10,286a] strengthened this criterion by showing that for every $\epsilon >0$ there is an $N_0(\epsilon)$ such that if the $N$th partial sum

$$\sum_{n=1}^N n^{-s}$$

of the zeta-function has no zeros in $\sigma> 1+N^{-1/2+\epsilon}$ for all $N>N_0(\epsilon)$ then the Riemann Hypothesis holds.

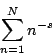
H. Montgomery [ MR 87a:11081] proved that this approach cannot work because for any positive number $c< 4/\pi-1$ the $N$th partial sum of $\zeta(s)$ has zeros in the half-plane

$$\sigma > 1+c (\log \log N) /\log N.$$

Back to the main index for The Riemann Hypothesis.