The Beurling-Nyman Criterion

In his 1950 thesis [ MR 12,108g], B. Nyman, a student of A. Beurling, proved that the Riemann Hypothesis is equaivalent to the assertion that $\mathcal N_{(0,1)}$ is dense in $L^2(0,1).$ Here, $\mathcal N_{(0,1)}$ is the space of functions

$$f(t)=\sum_{k=1}^n c_k \rho(\theta_k/t)$$

for which $\theta_k\in (0,1)$ and such that $\sum_{k=1}^n c_k=0$.

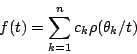
Beurling [ MR 17,15a] proved that the following three statements regarding a number $p$ with $1<p<\infty$ are equivalent:

(1) $\zeta(s)$ has nozeros in $\sigma>1/p$

(2) $\mathcal N_{(0,1)}$ is dense in $L^p(0,1)$ (3) The characteristic function $\chi_{(0,1)}$ is in the closure of $\mathcal N_{(0,1)}$ in $L^p(0,1)$

Back to the main index for The Riemann Hypothesis.