By the Euler Product, the ![]() -function
-function ![]() does
not vanish in the half-plane
does
not vanish in the half-plane ![]() . Thus, the simplest
nontrivial assertion about the zeros of
. Thus, the simplest
nontrivial assertion about the zeros of ![]() is that
is that
![]() does not vanish on the
does not vanish on the ![]() line. Such a result
is known as a Prime Number Theorem for
line. Such a result
is known as a Prime Number Theorem for ![]() .
The name arises as follows. The classical Prime Number Theorem(PNT):
.
The name arises as follows. The classical Prime Number Theorem(PNT):
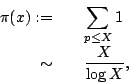
The Prime Number Theorem for ![]() was proven by Hadamard
and de la Valee Poissin in 1896. Jacquet and Shalika [55 #5583]
proved the corresponding result for
was proven by Hadamard
and de la Valee Poissin in 1896. Jacquet and Shalika [55 #5583]
proved the corresponding result for ![]() -functions associated to
automorphic representations on
-functions associated to
automorphic representations on ![]() . It would be significant
to prove such a result for the Selberg Class.
. It would be significant
to prove such a result for the Selberg Class.
Back to the
main index
for The Riemann Hypothesis.