Dirichlet series associated with holomorphic cusp forms
Level one modular forms. A cusp form of weight 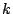 for the full modular group is
a holomorphic function
for the full modular group is
a holomorphic function 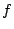 on the upper half-plane which satisfies
on the upper half-plane which satisfies
for all integers 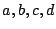 with
with 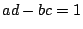 and also has the
property that
and also has the
property that
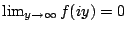 . Cusp forms for the
whole modular group exist only for even integers
. Cusp forms for the
whole modular group exist only for even integers 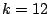 and
and 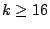 . The cusp forms of a given weight
. The cusp forms of a given weight 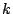 of this form make a
complex vector space
of this form make a
complex vector space 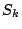 of dimension
of dimension ![$[k/12]$](img10.gif) if
if
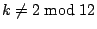 and of dimension
and of dimension ![$[k/12]-1$](img12.gif) if
if 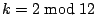 . Each such vector
space has a special basis
. Each such vector
space has a special basis 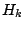 of Hecke eigenforms which consist
of functions
of Hecke eigenforms which consist
of functions
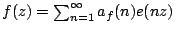 for which
for which
The Fourier coefficients 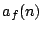 are real algebraic integers of
degree equal to the dimension of the vector space
are real algebraic integers of
degree equal to the dimension of the vector space 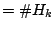 . Thus,
when
. Thus,
when
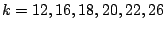 the spaces are one dimensional
and the coefficients are ordinary integers.
The L-function associated with a Hecke form
the spaces are one dimensional
and the coefficients are ordinary integers.
The L-function associated with a Hecke form 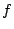 of weight
of weight 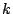 is
given by
is
given by
By Deligne's theorem
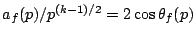 for
a real
for
a real 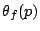 . It is conjectured (Sato-Tate) that for each
. It is conjectured (Sato-Tate) that for each
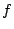 the
the
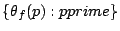 is uniformly distributed
on
is uniformly distributed
on 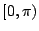 with respect to the measure
with respect to the measure
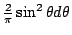 . We write
. We write
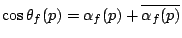 where
where
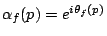 ; then
; then
The functional equation satisfied by 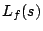 is
is
Higher level forms. Let 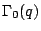 denote the group of matrices
denote the group of matrices
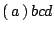 with integers
with integers 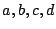 satisfying
satisfying 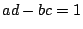 and
and 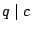 . This group is called the Hecke congruence group.
A function
. This group is called the Hecke congruence group.
A function 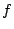 holomorphic on the upper half plane satisfying
holomorphic on the upper half plane satisfying
for all matrices in 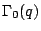 and
and
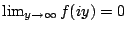 is called a cusp form for
is called a cusp form for 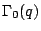 ; the space of these is a finite dimensional vector space
; the space of these is a finite dimensional vector space 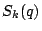 . The space
. The space 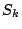 above is the same as
above is the same as 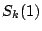 . Again, these spaces are empty unless
. Again, these spaces are empty unless 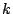 is an even integer. If
is an even integer. If 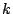 is an even integer, then
is an even integer, then
where 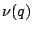 is the index of the subgroup
is the index of the subgroup 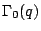 in the full modular group
in the full modular group 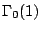 :
:
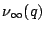 is the number of cusps of
is the number of cusps of 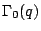 :
:
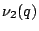 is the number of inequivalent elliptic points of order 2:
is the number of inequivalent elliptic points of order 2:
and 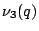 is the number of inequivalent elliptic points of order 3:
is the number of inequivalent elliptic points of order 3:
It is clear from this formula that the dimension of 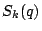 grows approximately linearly with
grows approximately linearly with 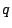 and
and 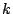 .
.
For the spaces 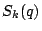 the issue of primitive forms and imprimitive forms arise, much as the situation with characters.
In fact, one should think of the Fourier coefficients of cusp forms as being a generalization of characters. They are not periodic, but they act as harmonic detectors, much as characters do, through their orthogonality relations (below).
Imprimitive cusp forms arise in two ways. Firstly , if
the issue of primitive forms and imprimitive forms arise, much as the situation with characters.
In fact, one should think of the Fourier coefficients of cusp forms as being a generalization of characters. They are not periodic, but they act as harmonic detectors, much as characters do, through their orthogonality relations (below).
Imprimitive cusp forms arise in two ways. Firstly , if
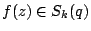 , then
, then
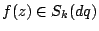 for any integer
for any integer 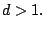 Secondly, if
Secondly, if
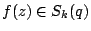 , then
, then
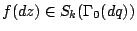 for any
for any 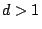 .
The dimension of the subspace of primitive forms is given by
.
The dimension of the subspace of primitive forms is given by
where 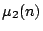 is the multiplicative function defined for prime powers by
is the multiplicative function defined for prime powers by 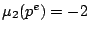 if
if 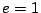 ,
, 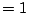 if
if 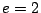 , and
, and 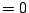 if
if 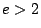 . The subspace of newforms has a Hecke basis
. The subspace of newforms has a Hecke basis 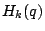 consisting of primitive forms, or newforms, or Hecke forms. These can be identified as those
consisting of primitive forms, or newforms, or Hecke forms. These can be identified as those 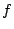 which have a Fourier series
which have a Fourier series
where the 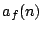 have the property that the associated L-function has an Euler product
have the property that the associated L-function has an Euler product
The functional equation satisfied by 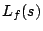 is
is
Back to the
main index
for The Riemann Hypothesis.
![]() for the full modular group is
a holomorphic function
for the full modular group is
a holomorphic function ![]() on the upper half-plane which satisfies
on the upper half-plane which satisfies
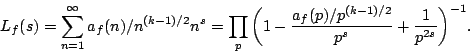
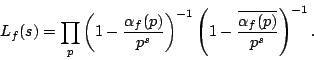
![]() denote the group of matrices
denote the group of matrices
![]() with integers
with integers ![]() satisfying
satisfying ![]() and
and ![]() . This group is called the Hecke congruence group.
A function
. This group is called the Hecke congruence group.
A function ![]() holomorphic on the upper half plane satisfying
holomorphic on the upper half plane satisfying
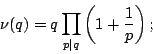
![]() grows approximately linearly with
grows approximately linearly with ![]() and
and ![]() .
.
![]() the issue of primitive forms and imprimitive forms arise, much as the situation with characters.
In fact, one should think of the Fourier coefficients of cusp forms as being a generalization of characters. They are not periodic, but they act as harmonic detectors, much as characters do, through their orthogonality relations (below).
Imprimitive cusp forms arise in two ways. Firstly , if
the issue of primitive forms and imprimitive forms arise, much as the situation with characters.
In fact, one should think of the Fourier coefficients of cusp forms as being a generalization of characters. They are not periodic, but they act as harmonic detectors, much as characters do, through their orthogonality relations (below).
Imprimitive cusp forms arise in two ways. Firstly , if
![]() , then
, then
![]() for any integer
for any integer ![]() Secondly, if
Secondly, if
![]() , then
, then
![]() for any
for any ![]() .
The dimension of the subspace of primitive forms is given by
.
The dimension of the subspace of primitive forms is given by
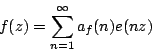
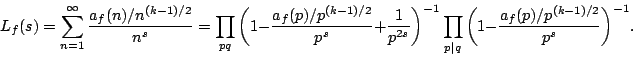
![]() is
is