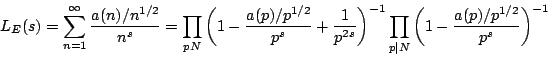Examples
See the [website]
for many specific examples.
Ramanujan's tau-function defined implicitly by
also yields the simplest cusp form. The associated Fourier series
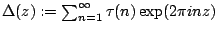 satisfies
satisfies
for all integers 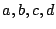 with
with 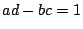 which means that it is a cusp form of weight 12 for the full modular group.
which means that it is a cusp form of weight 12 for the full modular group.
The unique cusp forms of weights 16, 18, 20, 22, and 26 for the full modular group can be given
explicitly in terms of (the Eisenstein series)
and
where 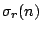 is the sum of the
is the sum of the 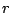 th powers of the positive
divisors of
th powers of the positive
divisors of 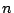 :
:
Then,
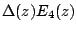 gives the unique Hecke form of weight 16;
gives the unique Hecke form of weight 16;
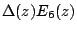 gives the unique Hecke form of weight 18;
gives the unique Hecke form of weight 18;
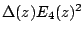 is the Hecke form of weight 20;
is the Hecke form of weight 20;
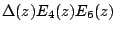 is the Hecke form of weight 22; and
is the Hecke form of weight 22; and
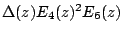 is the Hecke form of weight 26. The two
Hecke forms of weight 24 are given by
is the Hecke form of weight 26. The two
Hecke forms of weight 24 are given by
where
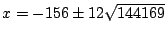 .
.
An example is the L-function associated to an elliptic
curve
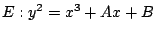 where
where 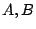 are integers.
The associated L-function, called the Hasse-Weil L-function, is
are integers.
The associated L-function, called the Hasse-Weil L-function, is
where 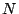 is the conductor of the curve. The coefficients
is the conductor of the curve. The coefficients 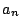 are constructed easily from
are constructed easily from 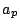 for prime
for prime 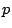 ; in turn the
; in turn the
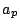 are given by
are given by 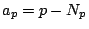 where
where 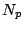 is the number of
solutions of
is the number of
solutions of 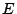 when considered modulo
when considered modulo 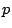 . The work of Wiles and
others proved that these L-functions are associated to modular
forms of weight 2.
. The work of Wiles and
others proved that these L-functions are associated to modular
forms of weight 2.
Back to the
main index
for The Riemann Hypothesis.
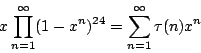
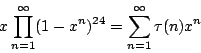
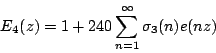
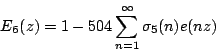
![]() where
where ![]() are integers.
The associated L-function, called the Hasse-Weil L-function, is
are integers.
The associated L-function, called the Hasse-Weil L-function, is