Charles Newman [MR 55 #7944],
building on work of deBruijn [
MR 12,250]
defined
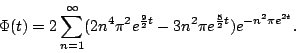
He proved that there exists a constant ![]() (with
(with
![]() ) such that
) such that
![]() has only real zeros if and only if
has only real zeros if and only if
![]() . RH is equivalent to the assertion that
. RH is equivalent to the assertion that ![]() .
.
The constant ![]() (which Newman conjectured is equal to 0) is now called the deBruijn-Newman constant. A. Odlyzko [
MR 2002a:30046] has recently proven that
(which Newman conjectured is equal to 0) is now called the deBruijn-Newman constant. A. Odlyzko [
MR 2002a:30046] has recently proven that
![]() .
.
Back to the
main index
for The Riemann Hypothesis.