Remarks on Agrawal's Conjecture

These notes concern Agrawal's conjecture, the first problem in the problem session:

Conjecture. Let $ n$ and $ r$ be two coprime positive integers. If

$\displaystyle (X-1)^n \equiv X^n - 1 \pmod{n,X^r-1} $

then either $ n$ is prime or

$\displaystyle n^2 \equiv 1 \pmod{r}. $

(If Agrawal's conjecture were true, this would improve the polynomial time complexity of the AKS primality testing algorithm from $ \widetilde{O}((\log n)^{7.5})$ to $ \widetilde{O}((\log n)^3)$.)

The contents are due to Lenstra and Pomerance and suggest strongly that this conjecture is false.

Proposition. [Lenstra] Let $ p_1,\dots,p_k$ be $ k$ pairwise distinct prime integers, and let $ n=p_1 \dots p_k$. Suppose that:

  1. $ k\equiv 1 \pmod{4}$;
  2. $ p_i \equiv 3 \pmod{80}$ for all $ i$;
  3. $ (p_i-1) \mid (n-1)$ for all $ i$; and
  4. $ (p_i+1) \mid (n+1)$ for all $ i$.
Then

$\displaystyle (X-1)^n \equiv X^n - 1 \pmod{n,X^5-1} $

and $ n^2 \not\equiv 1 \pmod{5}$.

Remark. This result is also true for $ k \equiv 3 \pmod{4}$.

Proof. By assumption we get $ n=3^k \equiv 3 \pmod{80}$ because $ 3^4 \equiv 1 \pmod{80}$. So $ n \equiv 3 \pmod{5}$ and then $ n^2 \not\equiv 1 \pmod{5}$.

We also have the following identity:

$\displaystyle (X-1,X^4+X^3+X^2+X+1,n)=(1) $

in the polynomial ring $ \mathbb{Z}[X]$. Hence, in order to prove the identity

$\displaystyle (X-1)^n \equiv X^n - 1 \pmod{n,X^5-1} $

it suffices to prove that

$\displaystyle (X-1)^n \equiv X^n-1 \pmod{n,X^4+\dots+X+1}. $

The Chinese remainder theorem gives the following isomorphism:

$\displaystyle \mathbb{Z}[X]/(n,X^4+\dots+X+1) \cong \prod_{i=1}^k \mathbb{F}_{p_i}[X]/(X^4+\dots+X+1). $

Each ring factor $ R_i = \mathbb{F}_{p_i}[X]/(X^4+\dots+X+1)$ is actually a field since each prime $ p_i$ is prime to $ 5$ and the $ 5$th cyclotomic polynomial is irreducible in $ \mathbb{F}_p[X]$ so that $ R_i$ is nothing but the splitting field of $ \mathbb{F}_{p_i}[\zeta_5]$ for a primitive $ 5$th root of unity $ \zeta_5$.

It therefore suffices to prove that each prime $ p_i=p$ satisfies

$\displaystyle (\zeta_5-1)^n=\zeta_5^n-1 $

in the field $ \mathbb{F}_p[\zeta_5]$. We see from (ii) that

$\displaystyle (\zeta_5-1)^{p^2}=\zeta_5^{p^2}-1=\zeta_5^{-1}-1 $

(since $ p\equiv 3 \pmod{5}$, we have $ p^2 \equiv -1 \pmod{5}$). Thus

$\displaystyle (\zeta_5-1)^{p^2}=-\zeta_5^{-1}(\zeta_5-1). $

Hence the order of $ (\zeta_5-1)$ in $ \mathbb{F}_p[\zeta_5]$ divides $ 10(p^2-1)$.

It remains to check the residue class of $ n$ modulo $ 10(p^2-1)$; more precisely, it suffices to show that

$\displaystyle n \equiv p \pmod{10(p^2-1)}. $

We can factor $ 10(p^2-1)$ into $ 4$ pairwise coprime factors:

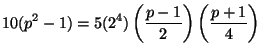
$\displaystyle 10(p^2-1)=5(2^4)\left(\frac{p-1}{2}\right)\left(\frac{p+1}{4}\right) $

so it suffices to verify this modulo each factor. Since $ n,p \equiv 3 \pmod{80}$ by assumption, the first follows. Assumption (iii) implies that

$\displaystyle n \equiv 1 \pmod{(p-1)/2} $

and so

$\displaystyle n=p \pmod{(p-1)/2} $

since $ p \equiv 1 \pmod{(p-1)/2}$, and

$\displaystyle n \equiv p\pmod{(p+1)/4} $

similarly. This completes the proof. $ \qedsymbol$

By this proposition, we have a heuristic which suggests the existence of many counterexamples to the Agrawal conjecture. This argument taken from analytic number theory is very similar to the one already used by Pomerance to find counterexamples to the Baillie-PSW primality testing algorithm which can be found at http://www.pseudoprime.com/dopo.pdf.

Fix some arbitrarily large integer $ m$ and let $ T$ be very large. Let $ P=P_m(T)$ denote the set of primes $ p$ in the interval $ [T,T^m]$ such that:

  1. $ p \equiv 3 \pmod{80}$;
  2. $ (p-1)/2$ is squarefree and divisible only by primes $ q \leq T$ with $ q \equiv 3 \pmod{4}$;
  3. $ (p+1)/4$ is squarefree and divisible only by primes $ r \leq T$ with $ r \equiv 1 \pmod{4}$.
Both smoothness conditions (2) and (3) are rather restrictive: heuristically, the cardinality of the set $ P$ is asymptotically ( $ T \to \infty$)

$\displaystyle \char93 P \sim c_m \frac{T^m}{(\log T^m)^2} $

for some positive constant $ c_m$ that depends on the choice of $ m$. In particular, we can take a sufficiently large integer $ T$ such that

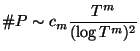
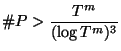
$\displaystyle \char93 P > \frac{T^m}{(\log T^m)^3} $

which we assume from now on.

Also choose an odd integer $ k\equiv 1 \pmod{4}$ such that $ k<T^2/(\log T^m)$. We consider the squarefree numbers $ n$ that run over products of $ k$ distinct primes of the set $ P$. Obviously such an integer $ n$ satisfies $ n<e^{T^2}$. The number of choices for $ n$ is exactly given by the binomial coefficient $ \binom{\char93 P}{k}$, and we get the lower bound:

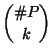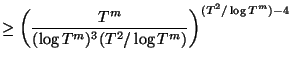$\displaystyle \binom{\char93 P}{k}$ $\displaystyle \geq \left(\frac{T^m}{(\log T^m)^3 (T^2/\log T^m)}\right)^{(T^2/\log T^m)-4}$    
  $\displaystyle > (T^{m-3})^{(T^2/\log T^m)-4} = e^{(1-3/m)T^2-4(m-3)\log T}$    
  $\displaystyle > e^{1-(4/m)T^2}.$    

for large $ T$ and fixed $ m$.

Let $ Q$ denote the product of primes $ q \leq T$ with $ q \equiv 3 \pmod{4}$, and let $ R$ denote the product of primes $ r \leq T$ with $ r \equiv 1 \pmod{4}$. Then $ Q$ and $ R$ are coprime and asymptotically the product $ QR$ equals $ e^{(1+o(1))T}$ as $ T \to \infty$, so that $ QR < e^{2T}$ for some large $ T$. Thus, the number of choices for the numbers $ n$ that satisfy in addition $ n \equiv 1 \pmod{Q}$ and $ n \equiv -1\pmod{R}$ should be asymptotically

$\displaystyle e^{(1-4/m)T^2} e^{-2T} > e^{T^2(1-5/m)}. $

But any such $ n$ is a counterexample to Agrawal's conjecture by Lenstra's proposition. We see therefore that for fixed $ m$ and for all large $ T$, there should be at least $ e^{T^2(1-5/m)}$ counterexamples to Agrawal's conjecture below $ e^{T^2}$. That is, if we let $ x=e^{T^2}$, this argument implies that the number of counterexamples $ \leq x$ is expected to be $ \gg x^{1-\epsilon}$ for any $ \epsilon>0$.



Back to the main index for Future directions in algorithmic number theory.