Given an 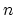 -dimensional smooth
projective variety
-dimensional smooth
projective variety 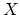 , we can study the canonical line bundle
, we can study the canonical line bundle 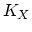 of holomorphic
of holomorphic 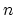 -forms. The dimensions of the spaces of global
sections of
-forms. The dimensions of the spaces of global
sections of
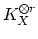 are useful birational invariants of
are useful birational invariants of
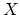 which aid in the classification of varieties (birational means
they only depend on a Zariski-open subset of
which aid in the classification of varieties (birational means
they only depend on a Zariski-open subset of 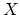 ). As
). As
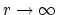 , these numbers either behave asymptotically like
, these numbers either behave asymptotically like
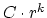 for a unique integer
for a unique integer 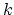 or are eventually zero. We define the
Kodaira dimension to be this integer
or are eventually zero. We define the
Kodaira dimension to be this integer 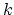 in the first case and
in the first case and
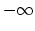 in the second case.
in the second case.
Another intepretation is as follows. For each 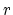 , we have a rational
map of
, we have a rational
map of 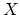 into projective space given by
into projective space given by
where
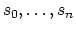 are the global sections of
are the global sections of
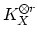 .
The Kodaira dimension is the supremum, as
.
The Kodaira dimension is the supremum, as
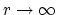 , of the
dimension of the image of
, of the
dimension of the image of 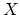 under these maps. Hence the Kodaira
dimension of
under these maps. Hence the Kodaira
dimension of 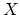 takes values in
takes values in
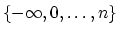 .
.
Jeffrey Herschel Giansiracusa
2005-06-27
![]() , we have a rational
map of
, we have a rational
map of ![]() into projective space given by
into projective space given by