A space 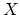 is an infinite loop
space if there is a sequence
is an infinite loop
space if there is a sequence
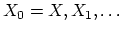 with homotopy
equivalences
with homotopy
equivalences
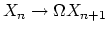 , i.e.
, i.e. 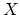 can be
de-looped arbitrarily many times. By adjunction, we have maps
can be
de-looped arbitrarily many times. By adjunction, we have maps
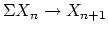 so
so 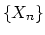 form a spectrum. Conversely
there is a functor from spectra to infinite loop spaces given by
sending a spectrum
form a spectrum. Conversely
there is a functor from spectra to infinite loop spaces given by
sending a spectrum
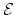 to
to
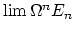 .
.
Jeffrey Herschel Giansiracusa
2005-06-27