Ratios of zeta-functions

A possible route to understanding the correlation functions of zeros of L-functions is via integrals of ratios of L-functions near the critical line. The simplest nontrivial case is the following formula conjectured by Farmer [ MR 95a:11076]. Suppose $u,v,a,b$ are of size $1/log(T)$ and $a,b$ have positive real part. It was conjectured that

$$\int_1^T {\zeta(\frac12+u+it)\zeta(\frac12+v-it)\over \zet... ...\left(1-T^{-(u+v)}\right)}{(u-a)(v-b)\over (u+v)(a+b)}\Biggr),$$

as $T\to\infty$.

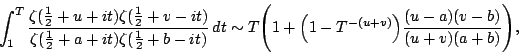
The above formula was obtained from a mollified mean value of the $\zeta$-function. This formula can be differentiated with respect to any of $u,v,a,b$, leading to other conjectures, such as for the mean 2nd and 4th moments of $\zeta'/\zeta$ near the critical line. This is useful because those moments are relevant in the study of the distribution of the prime numbers.

Combining the 2nd moment of $\zeta'/\zeta$ with work of Goldston, Gonek, and Montgomery, shows that the above formula implies Montgomery's pair correlation conjecture almost everywhere. This is interesting because the above formula was not explicitly based on any conjectures about the primes, nor did it obviously rely on any strong assumptions about the distribution of the zeros.

If the $\zeta$-functions in the above extression are replaced by the characteristic polynomial of a matrix from the Circular Unitary Ensemble and then averaged over the ensemble, the result agrees with the formula conjectured above. This suggests a way to conjecture more complicated versions if this formula, and may give a framework for a better understanding of which aspects of the zeros of $\zeta$-function should be governed by random matrix theory.

Recently Conrey, Farmer, Keating, and Snaith have shown that it is possible to use Dirichlet series techniques to conjecture generalizations of the above formula, both in terms of having more $\zeta$-functions and relaxing the restriction that $u,v,a,b$ be of size $1/\log T$. The results agree with the formulas obtained from random matrix theory. This could lead to a conjecture for the full main term in the $2k$th moment of the $\zeta$-function on the critical line.

It would be useful to fully understand the consequences of formulas like the one conjectured above, to find more formulas which give a clear connection with the GUE hypothesis, and to have a unified picture of the connection between various integrals of L-functions and the distribution of zeros. And, of course, it would be good to identify an approach which could lead to a proof of these formulas.

There is a formal similarity between the integrals of ratios of $\zeta$-functions and the ratios of $\Gamma$-functions in Barnes' type integrals. It may be that a natural object to study is an integral of ratios Riemann $\xi$-functions, which would include both $\Gamma$-factors and $\zeta$-function factors.

Back to the main index for L-functions and Random Matrix Theory.