Distribution of critical values
By considering the moments of
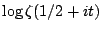 , Selberg (in unpublished work)
proved that for Borel measurable sets
, Selberg (in unpublished work)
proved that for Borel measurable sets 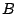 ,
,
which roughly speaking says that, high up the critical line,
the real and imaginary parts of
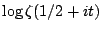 behave like
independent Gaussian random variables with mean zero and variance
behave like
independent Gaussian random variables with mean zero and variance
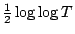 .
.
It is also of interest to look at the tails of this distribution,
for example the probability that
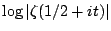 takes very
large negative values (which will be when
takes very
large negative values (which will be when
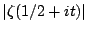 is very small).
One can make plausible conjectures about the behaviour of
is very small).
One can make plausible conjectures about the behaviour of
when 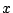 is very large, using methods of random matrix theory. In particular,
Hughes, Keating and O'Connell [Proc. R. Soc. Lond. 456, 2611--2627]
and Keating and Snaith [Comm. Math. Phys 214, 57--89]
have conjectured that for large
is very large, using methods of random matrix theory. In particular,
Hughes, Keating and O'Connell [Proc. R. Soc. Lond. 456, 2611--2627]
and Keating and Snaith [Comm. Math. Phys 214, 57--89]
have conjectured that for large 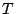 ,
,
where 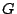 is the Barnes
is the Barnes 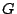 -function, and
-function, and 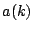 is a certain product
over primes, coming from mean values of
the
is a certain product
over primes, coming from mean values of
the 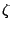 -function.
-function.
But much more is true (Hughes, PhD thesis). Writing 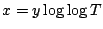 , then it is
conjectured that for large
, then it is
conjectured that for large 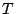 ,
,
uniformly for any 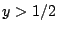 . The fact that
. The fact that 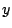 is restricted to
being greater than
is restricted to
being greater than
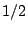 is important, since there is a phase transition there:
is important, since there is a phase transition there:
And thus we see a change in the behaviour of the left tail of
the distribution of
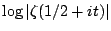 from the Gaussian decay
(anticipated from Selberg's result) to exponential decay.
from the Gaussian decay
(anticipated from Selberg's result) to exponential decay.
Back to the
main index
for L-functions and Random Matrix Theory.
![]() , Selberg (in unpublished work)
proved that for Borel measurable sets
, Selberg (in unpublished work)
proved that for Borel measurable sets ![]() ,
,
![\begin{displaymath}\lim_{T\to\infty} \frac{1}{T} meas
\left\{ t \in [0,T] : \fr...
...t\}=\frac{1}{2\pi} \int\!\!\!\int_B e^{-(x^2+y^2)/2}
\;dx \;dy\end{displaymath}](img3.gif)
![]() takes very
large negative values (which will be when
takes very
large negative values (which will be when
![]() is very small).
One can make plausible conjectures about the behaviour of
is very small).
One can make plausible conjectures about the behaviour of
![]() , then it is
conjectured that for large
, then it is
conjectured that for large ![]() ,
,