For convenience we state examples of the three main conjectures for moments in families. There are no open questions in this article (except how to prove these conjectures!). For simplicity, we state the conjectures only for integral moments.
Let
Conjecture.
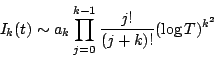
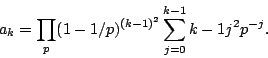
Let ![]() be a real, primitive, quadratic character to the modulus
be a real, primitive, quadratic character to the modulus ![]() (i.e. a Kronecker symbol)
and let
(i.e. a Kronecker symbol)
and let
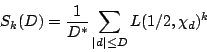
Conjecture.
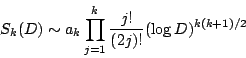
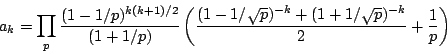
Let ![]() be a normalized newform of weight
be a normalized newform of weight ![]() and level
and level ![]() (where
(where ![]() is prime) (we write
is prime) (we write ![]() and let
and let ![]() be the associated
be the associated ![]() -function
(with critical strip
-function
(with critical strip ![]() .) Let
.) Let
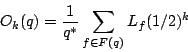
Conjecture.
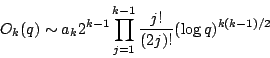
Back to the
main index
for L-functions and Random Matrix Theory.