Extremal problems

There are a collection of problems that go under this heading: the most basic is the question of the maximal size of the zeta-function on the critical line. There are basically two guesses for the answer - the larger or O-bound which follows from the Riemann Hypothesis and the smaller or omega result which in some cases can actually be proven. By ``omega result'' we mean an assertion of the form $f(t)=\Omega(g(t))$ as $t\to\infty$, which means that $\limsup_{t\to\infty} f(t)/g(t) > 0$.

For the case of the $\zeta$-function, on RH we have

$$\zeta(\frac12 + it) = O\left( \exp(c\log t/ \log\log t) \right)$$

for some $c> 0$, and

$$\zeta(\frac12 + it) = \Omega\left( \exp(c_1(\log t/\log \log t)^{1/2}) \right)$$

for some $c_1 > 0$

Traditional wisdom has favored the smaller bound. It seems to be the bound that is suggested by probability arguments. For example, one might think of $\log \zeta(\sigma+it)$ as being approximated by a sum $-\sum_{p\le x} p^{-\sigma-it}$ for an appropriate choice of $x$. How large can this sum be? It seems to depend on how well one can ``line up'' the small primes so that the $p^{it}$ are ``pointing'' in roughly the same direction. One can prove (Kronecker's theorem) that there exist $t$ for which the primes $p<\log t$ all have $\Re p^{it}>1/2$. But

$$\sum_{p\le x } p^{-1/2} \approx x^{1/2}/\log x.$$

With $x=\log t$ this bound is near the smaller bound.

On the other hand, the new conjectures for moments of the zeta-function may suggest that $\zeta(1/2+it)$ can be as big as the larger bound. One has

$$\max_{0\le t\le T}\vert\zeta(1/2+it)\vert \ge \left(\frac 1 T \int_0^T \vert\zeta(1/2+it)\vert^{2k}~dt\right)^{1/2k}.$$

If we substitute the conjectural asymptotic formula for the $2k$-th moment here and optimize over $k$ one is led to the bigger bound.

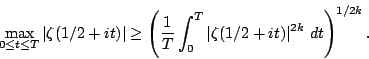
A seemingly related problem is the order of the $\zeta$-function on the 1-line. On RH we have

$$e^\gamma \le \limsup_{t\to\infty} \frac{\zeta(1+it)}{\log\log t} \le 2 e^\gamma .$$

Again, it would be interesting to determine which number, the larger or the smaller value, is correct.

Similar results (or conjectures) concern ranks of elliptic curves, Fourier coefficients of modular forms, and many other problems.

For each of these cases there is a similar paradigm: a larger and a smaller guess, and (properly interpreted) those two guesses differ by a factor of two. These problems are all based on the size of the value of an L-function, and it is possible that they naturally fall into one of two catagories, depending on whether the quantity in question naturally relates to a critical value of an $L$-function, or a non-critical value of an $L$-function. It is possible that for the problems related to critical values the larger guess is correct, while for non-critical values the smaller guess is correct. This change in behavior at the critical line was first suggested by Littlewood.

If there is indeed a fundamental distinction between the maximal size of critical vs. non-critical values, then it would also be important to understand the transition between those behaviors.

Back to the main index for L-functions and Random Matrix Theory.