The distribution of Fourier coefficients of half-integral weight forms
Let
be a newform of weight 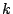 for the full modular group, and let
for the full modular group, and let
be a cusp form of weight  and level 4 which is associated to
and level 4 which is associated to 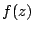 by the Shimura map. We normalize
by the Shimura map. We normalize 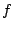 by requiring that
by requiring that 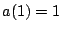 and we normalize
and we normalize 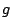 by requiring that
by requiring that
Then for squarefree 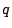 with
with
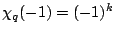 we have, by the formula of Kohnen and Zagier,
we have, by the formula of Kohnen and Zagier,
where
In particular, the Riemann Hypothesis for 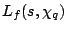 implies that
implies that
for an appropriate choice of 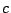 .
If the bound
.
If the bound
holds, then a similar bound for 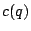 will hold (but with
will hold (but with 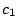 replaced by
replaced by 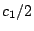 ).
The question here is to decide which (if either) of these bounds represents
the true state of affairs.
).
The question here is to decide which (if either) of these bounds represents
the true state of affairs.
If 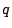 has a square factor, then
has a square factor, then 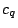 can be determined from values of
can be determined from values of 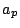 where
where  .
It is known, by Deligne's theorem, that
.
It is known, by Deligne's theorem, that
where 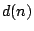 is the number of divisors of
is the number of divisors of 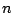 . Of course,
. Of course, 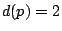 so
that we can write
so
that we can write
where 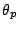 is real. The conjecture of Sato and Tate about the distribution of the
is real. The conjecture of Sato and Tate about the distribution of the 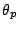 asserts that
asserts that
for
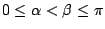 .
A consequence of the Sato-Tate conjecture is that there are infinitely many
.
A consequence of the Sato-Tate conjecture is that there are infinitely many 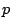 (actually a positive proportion of
(actually a positive proportion of 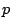 ) for which
) for which
for any given 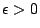 . The maximum order of
. The maximum order of 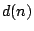 is given by
is given by
The Sato-Tate conjecture implies the same assertion with 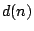 replaced by
replaced by
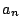 .
.
Thus, in particular, we find that
and we expect this bound to be sharp in the sense that the 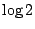 cannot be replaced by anything smaller.
cannot be replaced by anything smaller.
Thus, if the ``smaller'' bound is true for
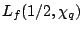 then there is a great variation between the distribution of the Fourier coefficients
then there is a great variation between the distribution of the Fourier coefficients 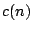 according to whether
according to whether 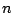 is square
or squarefree.
is square
or squarefree.
Back to the
main index
for L-functions and Random Matrix Theory.
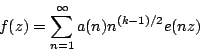
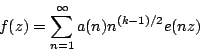
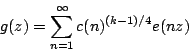
![]() has a square factor, then
has a square factor, then ![]() can be determined from values of
can be determined from values of ![]() where
where ![]() .
It is known, by Deligne's theorem, that
.
It is known, by Deligne's theorem, that
![]() then there is a great variation between the distribution of the Fourier coefficients
then there is a great variation between the distribution of the Fourier coefficients ![]() according to whether
according to whether ![]() is square
or squarefree.
is square
or squarefree.