Extreme gaps between consecutive zeros of the zeta-function
The number of zeros of 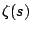 with imaginary parts smaller than
with imaginary parts smaller than 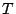 is given by
is given by
where
It is known that
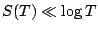 and, conditional on the Riemann Hypothesis that
and, conditional on the Riemann Hypothesis that
Thus, the average gap between zeros of 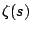 at height
at height 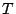 is
is
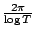 and
and 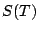 measures the local fluctuations in the zero spacings. (If not for
measures the local fluctuations in the zero spacings. (If not for 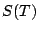 the zeros of
the zeros of 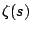 would have a `picket fence' spacing.)
would have a `picket fence' spacing.)
Clearly, a large gap between consecutive zeros of 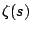 implies that
implies that 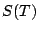 is correspondingly large. It seems not unreasonable to speculate that the largest gaps between consecutive zeros of
is correspondingly large. It seems not unreasonable to speculate that the largest gaps between consecutive zeros of 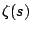 will `match' with the largest values of values of
will `match' with the largest values of values of 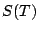 :
:
Thus, if 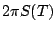 is occasionally as large as
is occasionally as large as
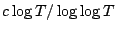 see the article on $S(T)$ then we would expect the maximal gaps between zeros of
see the article on $S(T)$ then we would expect the maximal gaps between zeros of 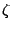 to be as large as
to be as large as 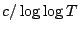 .
.
Back to the
main index
for L-functions and Random Matrix Theory.
![]() with imaginary parts smaller than
with imaginary parts smaller than ![]() is given by
is given by
![]() implies that
implies that ![]() is correspondingly large. It seems not unreasonable to speculate that the largest gaps between consecutive zeros of
is correspondingly large. It seems not unreasonable to speculate that the largest gaps between consecutive zeros of ![]() will `match' with the largest values of values of
will `match' with the largest values of values of ![]() :
: