Moments of the Riemann ![]() -function were introduced as a
tool to attack the
Lindelöff Hypothesis, which asserts that
-function were introduced as a
tool to attack the
Lindelöff Hypothesis, which asserts that
![]() for any
for any ![]() .
This is equivalent to
.
This is equivalent to
The above bound has only been established for ![]() and
and ![]() ,
and for those values an asymptotic formula is known for
the more general integral
,
and for those values an asymptotic formula is known for
the more general integral
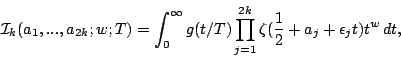
When ![]() or
or ![]() , the function
, the function
![]() can be continued to a meromorphic function. But
if
can be continued to a meromorphic function. But
if ![]() is larger, then
is larger, then
![]() is (conjecturally) not
continuable to a meromorphic function, and in fact it has a
natural boundary.
Diaconu, Goldfeld, and Hoffstein have shown that
the function continues to a sufficiently large region that
standard conjectures for the moments of
is (conjecturally) not
continuable to a meromorphic function, and in fact it has a
natural boundary.
Diaconu, Goldfeld, and Hoffstein have shown that
the function continues to a sufficiently large region that
standard conjectures for the moments of ![]() -functions should be
able to be
recovered from the polar divisors of
-functions should be
able to be
recovered from the polar divisors of
![]() .
However, the fact that the function under consideration is
not entire suggests that it may not be the correct object
to study.
.
However, the fact that the function under consideration is
not entire suggests that it may not be the correct object
to study.
Problem: Find a natural way to modify
![]() so that
it becomes an entire (meromorphic) function.
so that
it becomes an entire (meromorphic) function.
The fact that
![]() is not a nice function for
is not a nice function for ![]() is an aspect of the ``Estermann Phenomonon.'' Consider the
Dirichlet series
is an aspect of the ``Estermann Phenomonon.'' Consider the
Dirichlet series
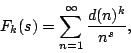
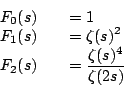
An example which may be more closely related to the situation at hand is
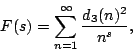
See Titchmarsh [ MR 88c:11049] for more background information.
Back to the
main index
for L-functions and Random Matrix Theory.