The order of $\zeta'/\zeta$
Assume the Riemann Hypothesis. Define 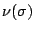 for
for 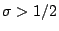 to be the greatest lower bound of the numbers
to be the greatest lower bound of the numbers 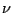 for which
for which
holds as 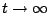 for all
for all 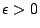 . It is a theorem that
. It is a theorem that 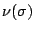 is a
convex function of
is a
convex function of 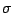 which is continuous and decreasing for
which is continuous and decreasing for 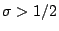 with
with 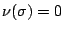 for all
for all 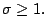 It can be shown that
It can be shown that
for
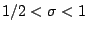 . There is an analogous function which can be defined for
. There is an analogous function which can be defined for
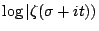 and it can be shown that this analogous function is,
in fact, equal to
and it can be shown that this analogous function is,
in fact, equal to 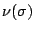 . See Titchmarsh for all of these facts.
Which bound is corrct?
. See Titchmarsh for all of these facts.
Which bound is corrct?
If the smaller bound is the correct one, then near the half-line we see that
for 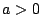 . On the other hand,
. On the other hand,
Thus, if the smaller bound holds, then there is a jump at 1/2. It could be that the
smaller bound holds to the right of the critical-line but that there is
radically different behavior on the critical line.
Back to the
main index
for L-functions and Random Matrix Theory.