Wednesday Discussion on Geometric Issues

This session was moderated by John Shareshian. The discussion started off with some comments about Riemannian metrics and whether the set of metrics on tree space would be useful to study.

• Vogtmann asked if this space may be too large to study?
• Forman noted that when geometers look at the space of all Riemannian metrics on a given space, they do it to try to find the ``best'' metric in some sense (e.g., such as one with constant curvature).

Q. Are there many useful or interesting metrics on tree space?

Q. Is the BHV metric the only one (up to scalars) of non-positive curvature? (Bridson)

• Charney: metrics are slightly different, but they should all be similar. If there is no reason that biologists suggest that one is better than another, then it makes sense to choose one that has useful properties, such as metrics of nonpositive curvature.

• Billera: for biologists, what metrics do you want to have on the orthants?

Q. What metrics ``should'' be used on the subspace obtained by fixing the tree type?

• St. John: uses the 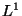$L^1$ metric, though Felsenstein uses $L^2$.
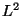• Penny: we use 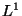$L^1$ because then lengths scale with time.
• Charney: since the data is not completely in tree space, maybe we should be considering non-intrinsic metrics.

• Forman: want to choose metrics so that the statistical methods we are using are continuous.

• Flath: perhaps some edges are more important than others?
• Penny: we are not surprised when we get edges near leaves are accurate, but we are really interested in getting deep internal edges right.

• Penny: taxonomic studies, just care about the branch order (weight 1 on edges), but when we consider time studies, we do want the lengths.

• Forman: measuring the residuals seem to imply that embedding tree space in some larger space and considering an extrinsic metric would be important.

• Vogtmann noted that Felsenstein was talking about embedding tree space in Euclidean space (using the Robinson-Foulds metric).

Q. How does the Robinson-Foulds metric compare with the BHV metric? (Diaconis) What's the Lipshitz constant? (Bridson)

• Vert: Another distance (referred to by Felsenstein in his talk) is Kullback-Leibler distance (relative entropy) between probabilities. Fix a model. Each tree defines a probability on the set of assignments of letters (A,G,C,T) to leaves. Maximum likelihood corresponds to projection of the empirical measure of a data point to tree space according to this distance.

  There was some explanation and discussion of this embedding. Diaconis noted that while there are many metrics on probability distributions to consider here, the Kullback-Liebler separation is good for maximum likelihood.

Q. Should the metric on tree space come from an intrinsic metric, or an extrinsic metric on a larger space in which tree space is embedded? Which is a more natural way to view tree space?

• Forman: studying the residuals seems to be very important. This larger space is part of what you are given in the data, and should be useful. Charney rephrased the question as: what is the right ambient space to embed tree space? While Bridson remarked that he viewed tree space as God-given, Forman asserted that he views the data as God-given.

• Vert remarked that the ``average'' of trees with high likelihood may not be high likelihood with the intrinsic metric.

Q. How do you deliver geometry to biologists? (Billera)

• Billera pointed out that interesting mathematics in biology seems to happen by serendipity-- cases in which someone happened to know some mathematics or knew someone who did.

• Penny: notes that there is a role for mathematics to play. Also new majors in mathematical biology (at some schools) have arisen that will train students to think in both disciplines.

• Diaconis notes that as a result of this conference, and ensuing discussions, people might write an article for Science. This may bring biologists to mathematics.

• Snel suggests advocating a notion of average, and communicate why it is better. For instance, articles on concatenated alignments have appeared in Science.

• Huelsenbeck: write review articles that explain things clearly. Write for Systematics Biology-- that's where stuff on trees would appear.

• Billera asked again how one spreads mathematical knowledge in the biological community, noting that courses offered at most institutions are either at too low or too high a level for biologists.

Back to the main index for Geometric models of biological phenomena.