Monday Discussion on Combinatorial Issues
The disussion was moderated by Michelle Wachs. She started off the
discussion by asking:
Q. What combinatorial questions arise in biology that might be of
interest to biologists? Or, what problems motivated by biology would
be of interest to mathematicians, to give us some interesting problems?
- Huelsenbeck:
In putting priors on the set of all possible trees, we sometimes need
to count trees with
particular characteristics, such as ones with a particular kind
of edge (split, bipartition), or a list of either this or that kind of
edge. The constraints may be multiple or conflicting. The count is
needed so that we can sum probabilities over these trees.
- Holmes pointed out that inclusion/exclusion issues are involved here.
There was some discussion about NP-hard problems, but Billera pointed
out that complexity issues are not that relevant for the basic question of how
to count these things.
Q. Given a set 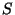 of
of 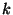 edges, and a subset
edges, and a subset 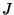 of
of 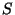 ,
how many leaf labeled binary trees have some subset
,
how many leaf labeled binary trees have some subset 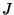 of
of 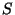 but not the edges in
but not the edges in 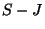 ? Do this for all
? Do this for all 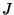 .
.
- Evans asked why we can't just use MCMC to solve this problem?
Holmes pointed out that the combinatorics may give some insight.
- Another example of a question that arises:
the number of trees that are distance
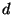 from a particular set of trees
(e.g., using a distance such as nearest-neighbor interchange)?
from a particular set of trees
(e.g., using a distance such as nearest-neighbor interchange)?
Q. What are good codings for trees?
- Wachs described a bijection between phylogenetic trees and type B
permutations whose left-to-right minimum is unbarred.
(Type B permutations are permutations in which each number can be
barred or unbarred.) This can be used as a coding for trees.
- There was a question about Penny's method for coding trees
(in which each time you add an edge there are
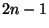 places to add it, so
that you get
places to add it, so
that you get 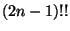 of them). Billera said that this is the same as
what was on the board.
of them). Billera said that this is the same as
what was on the board.
- Penny mentioned the existence of
another scheme for coding each tree by a unique number.
Holmes pointed out that the biologists use a
Newick notation (New Hampshire format) that uses lots of parentheses.
Another coding is a matrix where the columns are edges, and the rows
are vertices, and you put a 1 if the edge is an ancestor of the
vertex. (Brooks used it in biology, and Graham-Winkler used
for addressing a network).
- Holmes described a
matching representation is one due to Diaconis-Holmes.
When
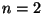 there is one matching,
when
there is one matching,
when 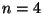 there are 3 matchings,
when
there are 3 matchings,
when 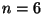 there are 15 matchings, corresponding to 4 leaf trees.
The matchings are the sibling pairs. Example:
there are 15 matchings, corresponding to 4 leaf trees.
The matchings are the sibling pairs. Example: 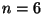 . Call the numbers
from 1 to 4 available numbers, and the other numbers unavailable.
Given a matching
. Call the numbers
from 1 to 4 available numbers, and the other numbers unavailable.
Given a matching
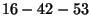 , pick the first available pair of numbers.
By pigeonhole argument, there is some pair, that's a sibling
pair in a tree. Then the smallest non-available number (5, in this
case) is the parent, and the other member of the pair (3) is the
sibling of 5. Continue.
, pick the first available pair of numbers.
By pigeonhole argument, there is some pair, that's a sibling
pair in a tree. Then the smallest non-available number (5, in this
case) is the parent, and the other member of the pair (3) is the
sibling of 5. Continue.
- Diaconis pointed out their matching method is
related to Billera's method using Prufer codes.
Q. Is there an efficient representation for coding trees? (Billera)
Q. Is there a nice neat notation for trees that is continuous when
doing a random walk on trees? In other words, do small changes in
notation correspond to close trees?
(Diaconis)
- The type B permutation coding might be very amenable to doing a
random walk. Bridson pointed out that this
representation is related to subsets of the Cayley graph of the Weyl group.
Q. Are there questions that combinatorialists might have for biologists?
Combinatorial structures that biologists might be interesting?
(Wachs)
Q. If we took trees and instead of putting real numbers of
them, putting discrete values, like 0-1, would that be of interest in
biologists? (Diaconis)
- Huelsenbeck: this
maybe useful in character-mapping, mapping characters that are on or off.
Perhaps some substitutions are more likely when characters are on.
- Epstein: it certainly
seems reasonable to associate to each edge a vector, rather than a real number.
- Evans: as in Penny's talk,
characters of each of the vertices can be thought of as
elements of the Klein 4-group... the edges can represent differences
of elements at the vertices.
- Wachs: what about
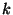 -ary trees?
-ary trees?
- Penny: people find cycles useful for representing uncertainty.
Referred to some who tried to define
how tree-like the data was, something tree-like would have only small cycles.
- Holmes referred to a program called splitstree that makes such diagrams.
- Penny: biologist would like structures that represents distances
accurately.
- Shareshian: described a space that arose in his work, a space in which
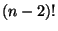 cycles correspond to associahedra.
cycles correspond to associahedra.
Back to the
main index
for Geometric models of biological phenomena.
![]() of
of ![]() edges, and a subset
edges, and a subset ![]() of
of ![]() ,
how many leaf labeled binary trees have some subset
,
how many leaf labeled binary trees have some subset ![]() of
of ![]() but not the edges in
but not the edges in ![]() ? Do this for all
? Do this for all ![]() .
.